
【题目】(10分)直线y=x﹣6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF∥AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x﹣6与坐标轴交点坐标是A( , ),B( , );
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);

【答案】(1)①A(6,0),B(0,﹣6);②见解析;(2)t=12﹣6![]()
【解析】整体分析:
(1)①分别把x=0,y=0代入方程y=x﹣6,可得A,B的坐标;②先确定点E,F的坐标,再根据轴对称的性质,确定点A,B关于EF的对称点D,C的坐标;(2)用两组对边分别平行的四边形是平行四边形证明四边形DHEF为平行四边形,由DF=EF列方程求解.
解:(1)①当y=0,x﹣6=0,解得x=6;
当x=0时,y=-6.
所以直线y=x﹣6与坐标轴交点坐标是:A(6,0),B(0,﹣6);
②如图1,四边形DCEF即为四边形ABEF沿EF折叠后的图形;
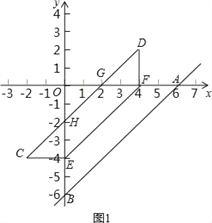
(2)∵四边形DCEF与四边形ABEF关于直线EF对称,
又AB∥EF,∴CD∥EF.
∵OA=OB,∠AOB=90°,∴∠BAO=45°.
∵AB∥EF,∴∠AFE=135°,∴∠DFE=∠AFE=135°.
∴∠AFD=360°﹣2×135°=90°,即DF⊥x轴.
∴DF∥EH,
∴四边形DHEF为平行四边形.
要使四边形DHEF为菱形,
只需EF=DF,
∵AB∥EF,∠FAB=∠EBA,∴FA=EB.
∴DF=FA=EB=t.
又∵OE=OF=6﹣t,∴EF=![]() (6-t).
(6-t).
∴![]() (6-t)=t.
(6-t)=t.
∴t=![]() =12﹣
=12﹣![]() .
.
∴当t=12﹣![]() 时,四边形DHEF为菱形.
时,四边形DHEF为菱形.



科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线. 
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,水坝的横断面是梯形,背水坡AB的坡角∠BAD=60°,坡长AB=20 ![]() m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据:
m,为加强水坝强度,降坝底从A处后水平延伸到F处,使新的背水坡角∠F=45°,求AF的长度(结果精确到1米,参考数据: ![]() 1.414,
1.414, ![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t天完成.
(1)写出每天生产夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;
(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据实际意义可列出夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;
(2)根据题意列出t﹣4对应的式子![]() ,与(1)中的式子相减即可.
,与(1)中的式子相减即可.
试题解析:(1)由题意可得,函数关系式为:w=![]() (
(![]() );
);
(2)![]() =
=![]() =
=![]() .(或
.(或![]() ).
).
答:每天多做![]() (或
(或![]() )件夏凉小衫才能完成任务.
)件夏凉小衫才能完成任务.
考点:反比例函数的应用.
【题型】解答题
【结束】
13
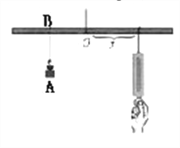
【题目】如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况。实验数据记录如下:
x(cm) | … | 10 | 15 | 20 | 25 | 30 | … |
y(N) | … | 30 | 20 | 15 | 12 | 10 | … |
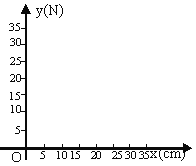
(1)把上表中x,y的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点并观察所得的图象,猜测y(N)与x(cm)之间的函数关系,并求出函数关系式;
(2)当弹簧秤的示数为24N时,弹簧秤与O点的距离是多少cm?
随着弹簧秤与O点的距离不断减小,弹簧秤上的示数将发生怎样的变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为 ![]() .其中,正确的结论是( )
.其中,正确的结论是( ) 
A.①②④
B.①③⑤
C.②③④
D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的盒子里有背面完全相同,正面上分别写有数字1、2、3、4的四张卡片,小马从中随机地抽取一张,把卡片上的数字作为被减数;在另一只不透明的盒子里将形状、大小完全相同,分别标有数字1、2、3的三个小球混合后,小虎从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小马与小虎做游戏,规则是:若这两数的差为非正数,则小马赢;否则小虎赢.你认为该游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
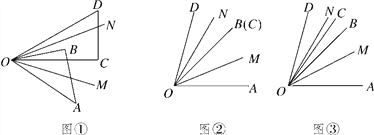
【题目】如图①,将一副三角板的两个锐角顶点放到一块,∠AOB=45°,∠COD=30°,OM,ON分别是∠AOC,∠BOD的平分线.
(1)当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图②),则∠MON的大小为________;
(2)如图③,在(1)的条件下,继续绕着点O逆时针旋转∠COD,当∠BOC=10°时,求∠MON的大小,写出解答过程;
(3)在∠COD绕点O逆时针旋转过程中,∠MON=________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2015秒时,点P的坐标是( )
个单位长度,则第2015秒时,点P的坐标是( )
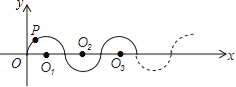
A. (2014,0) B. (2015,﹣1) C. (2015,1) D. (2016,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生开展踢毽子比赛活动,每班派5名学生参加.按团体总分多少排列名次.在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)

请你回答下列问题:
(1)填写表格;
(2)根据以上信息,请你回答下列问题:
①从平均数、众数相结合的角度分析,应该把冠军奖状发给哪一个班级?
②从优秀率的角度分析,应该把冠军奖状发给哪一个班级?
(3)如果两个班各选两名同学参加市踢毽子的比赛,你认为哪个班级团体实力更强?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com