
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖl1”Ķl2£¬”ŃOÓėl1£¬l2¶¼ĻąĒŠ£¬”ŃOµÄ°ė¾¶ĪŖ2cm£®¾ŲŠĪABCDµÄ±ßAD£¬AB·Ö±šÓėl1£¬l2ÖŲŗĻ£¬AB£½![]() cm£¬AD£½4cm£®Čō”ŃOÓė¾ŲŠĪABCDŃŲl1Ķ¬Ź±ĻņÓŅŅĘ¶Æ£¬”ŃOµÄŅʶÆĖŁ¶ČĪŖ3cm/s£¬¾ŲŠĪABCDµÄŅʶÆĖŁ¶ČĪŖ4cm/s£¬ÉčŅĘ¶ÆŹ±¼äĪŖt(s)£®
cm£¬AD£½4cm£®Čō”ŃOÓė¾ŲŠĪABCDŃŲl1Ķ¬Ź±ĻņÓŅŅĘ¶Æ£¬”ŃOµÄŅʶÆĖŁ¶ČĪŖ3cm/s£¬¾ŲŠĪABCDµÄŅʶÆĖŁ¶ČĪŖ4cm/s£¬ÉčŅĘ¶ÆŹ±¼äĪŖt(s)£®
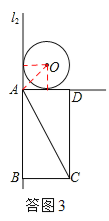
(1)ČēĶ¼¢Ł£¬Į¬½ÓOA£¬AC£¬Ōņ”ĻOACµÄ¶ČŹżĪŖ ”ć£»
(2)ČēĶ¼¢Ś£¬Į½øöĶ¼ŠĪŅʶÆŅ»¶ĪŹ±¼äŗ󣬔ŃOµ½“ļ”ŃO1µÄĪ»ÖĆ£¬¾ŲŠĪABCDµ½“ļA1B1C1D1µÄĪ»ÖĆ£¬“ĖŹ±µćO1£¬A1£¬C1Ē”ŗĆŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬ĒóŌ²ŠÄOŅĘ¶ÆµÄ¾ąĄė(¼“OO1µÄ³¤£©£»
(3)ŌŚŅĘ¶Æ¹ż³ĢÖŠ£¬Ō²ŠÄOµ½¾ŲŠĪ¶Ō½ĒĻßACĖłŌŚÖ±ĻߵľąĄėŌŚ²»¶Ļ±ä»Æ£¬ÉčøĆ¾ąĄėĪŖd(cm)£®µ±d<2Ź±£¬ĒótµÄȔֵ·¶Ī§£®£Ø½ā“šŹ±æÉŅŌĄūÓƱøÓĆĶ¼»³öĻą¹ŲŹ¾ŅāĶ¼£©

”¾“š°ø”æ£Ø1£©105£»£Ø2£©![]() £»£Ø3£©
£»£Ø3£©![]() £¼t£¼
£¼t£¼![]() .
.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©”ŃOÓėl1£¬l2¶¼ĻąĒŠ£¬Į¬½ÓŌ²ŠÄŗĶĮ½øöĒŠµć£¬µČÕż·½Ļņ.OA¼“ĪŖÕż·½ŠĪµÄ¶Ō½ĒĻߣ¬µĆµ½”ĻOAD=450£¬ŌŁŌŚRt”÷ADCÖŠ£¬ÓÉČń½ĒČż½ĒŗÆŹżĒó”ĻDAC=600£¬“Ó¶ųĒóµĆ”ĻOACµÄ¶ČŹż1050.
£Ø2£©Į¬½ÓO1ÓėĒŠµćE£¬ŌņO1E=2£¬O1E”Ķl1£¬ĄūÓĆ”÷O1EA1”×”÷D1C1E1,ĒóA1E=![]() £¬øł¾Ż2+O1O+A1E=AA1£¬æÉĒót£¬½ų¶ųĒóµĆŌ²ŠÄŅĘ¶ÆµÄ¾ąĄė3t=
£¬øł¾Ż2+O1O+A1E=AA1£¬æÉĒót£¬½ų¶ųĒóµĆŌ²ŠÄŅĘ¶ÆµÄ¾ąĄė3t=![]() .
.
£Ø3£©Ō²ŠÄOµ½¶Ō½ĒĻßACµÄ¾ąĄėd£¼2£¬¼“d£¼r.ĖµĆ÷”ŃOÓėACĻą½»£¬ĖłŅŌ³öÕŅĮ½øöĮŁ½ēµćµÄtÖµ£¬¼“”ŃOÓėACĻąĒŠ£®ŌĖ¶ÆÖŠ“ęŌŚĮ½øöĻąĒŠµÄĪ»ÖĆ.·Ö±šĒóĮ½øöĻąĒŠŹ±tµÄÖµ£¬¼“æÉµĆ³öd£¼rŹ±£¬tµÄȔֵ
ŹŌĢā½āĪö£ŗ½ā£ŗ£Ø1£©1050.
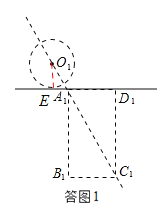
£Ø2£©O1£¬A1£¬C1Ē”ŗĆŌŚĶ¬Ņ»Ö±ĻßÉĻŹ±£¬Éč”ŃOÓėACµÄĒŠµćĪŖE£¬Į¬½ÓO1E£¬Čē“šĶ¼1£¬
æɵĆO1E=2£¬O1E”Ķl1£¬
ŌŚRt”÷A1D1C1ÖŠ£¬”ßA1D1=4£¬D1C1=![]() £¬
£¬
”ątan”ĻC1A1D1=![]() £®”ą”ĻC1A1D1=600£®
£®”ą”ĻC1A1D1=600£®
ŌŚRt”÷A1O1EÖŠ, ”ĻO1A1E=”ĻC1A1D1=600£®”ąA1E=![]() ,
,
”ß![]() £¬”ą
£¬”ą![]() £¬”ą
£¬”ą![]() .
.
”ąOO1=3t=![]() .
.
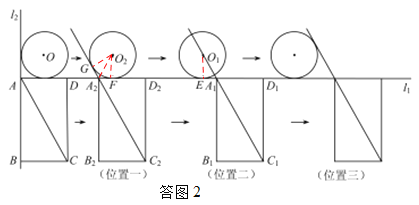
£Ø3£©Čē“šĶ¼2£¬
¢Łµ±Ö±ĻßACÓė”ŃOµŚŅ»“ĪĻąĒŠŹ±£¬ÉčŅĘ¶ÆŹ±¼äĪŖt1.ČēĪ»ÖĆŅ»£¬“ĖŹ±”ŃOŅĘ¶Æµ½”ŃO2µÄĪ»ÖĆ£¬¾ŲŠĪABCDŅĘ¶Æµ½A2B2C2D2µÄĪ»ÖĆ.
Éč”ŃO2ÓėÖ±Ļßl1”¢A2C2·Ö±šĻąĒŠÓŚµćF”¢G, Į¬½ÓO2F”¢O2G”¢O2A2£¬
”ąO2F”Ķl1”¢O2G”ĶA2C2.
ÓÖÓÉ£Ø2£©æɵƔĻC2A2D2=600ÓŚ£¬”ą”ĻGA2F=1200£®”ą”ĻO2A2F=600.
ŌŚRt”÷O2A2FÖŠ£¬O2F=2£¬”ąA2F=![]() .
.
”ßOO2=3t1£¬ ![]() £¬”ą
£¬”ą![]() £¬½āµĆ
£¬½āµĆ![]() .
.
¢Śµ±µćO1£¬A1£¬C1Ē”ŗĆŌŚĶ¬Ņ»Ö±ĻßÉĻŹ±ĪŖĪ»Öƶž£¬ÉčŅĘ¶ÆŹ±¼äĪŖt2.ÓÉ£Ø2£©æɵĆ![]() .
.
¢Ūµ±Ö±ĻßACÓė”ŃOµŚ¶ž“ĪĻąĒŠŹ±£¬ÉčŅĘ¶ÆŹ±¼äĪŖt3£®ČēĪ»ÖĆ3£¬ÓÉĢāŅāÖŖ£¬“ÓĪ»ÖĆŅ»µ½Ī»ÖƶžĖłÓĆŹ±¼äÓėĪ»Öƶžµ½Ī»ÖĆČżĖłÓĆŹ±¼äĻąµČ.
”ą![]() £¬¼“
£¬¼“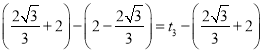 £¬½āµĆ
£¬½āµĆ![]() .
.
×ŪÉĻĖłŹö£¬µ±d<2Ź±£¬tµÄȔֵ·¶Ī§ĪŖ![]() £¼t£¼
£¼t£¼![]() .
.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖAC”ĶBC£¬BD”ĶAD£¬AC ÓėBD ½»ÓŚO£¬AC=BD£®
ĒóÖ¤£ŗ£Ø1£©BC=AD£»
£Ø2£©”÷OABŹĒµČŃüČż½ĒŠĪ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµćA£Ø3£¬©5£©ĻņÉĻĘ½ŅĘ4øöµ„Ī»£¬ŌŁĻņ×óĘ½ŅĘ3øöµ„Ī»µ½µćB£¬ŌņµćBµÄ×ų±źĪŖ£Ø””””£©
A.£Ø1£¬©8£©B.£Ø1£¬©2£©C.£Ø©7£¬©1£©D.£Ø0£¬©1£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ņ»“ĪŗÆŹżµÄĶ¼Ļó¾¹żµć![]() £¬ĒŅÓėÕż±ČĄżŗÆŹż
£¬ĒŅÓėÕż±ČĄżŗÆŹż![]() µÄĶ¼ĻóĻą½»ÓŚµć
µÄĶ¼ĻóĻą½»ÓŚµć![]() £¬ÓėxÖįĻą½»ÓŚµć
£¬ÓėxÖįĻą½»ÓŚµć![]()
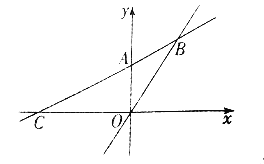
£Ø1£©ĒómµÄÖµ¼°Ņ»“ĪŗÆŹżµÄ±ķ“ļŹ½.
£Ø2£©Ēó”÷BOCµÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijøöÕżŹżµÄĮ½øöĘ½·½øłŹĒ2a©1ŗĶa©5£¬ŌņŹµŹżaµÄÖµĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø±¾Š”ĢāĀś·Ö10·Ö£©


¹Ū²ģĖ¼æ¼
ijÖÖŌŚĶ¬Ņ»Ę½Ćę½ųŠŠ“«¶ÆµÄ»śŠµ×°ÖĆČēĶ¼14-1£¬Ķ¼14-2ŹĒĖüµÄŹ¾ŅāĶ¼£®Ę乤×÷ŌĄķŹĒ£ŗ»¬æéQŌŚĘ½Ö±»¬µĄlÉĻæÉŅŌ×óÓŅ»¬¶Æ£¬ŌŚQ»¬¶ÆµÄ¹ż³ĢÖŠ£¬Į¬øĖPQŅ²ĖęÖ®ŌĖ¶Æ£¬²¢ĒŅPQ“ų¶ÆĮ¬øĖOPČĘ¹Ģ¶ØµćO°Ś¶Æ£®ŌŚ°Ś¶Æ¹ż³ĢÖŠ£¬Į½Į¬øĖµÄ½ÓµćPŌŚŅŌOPĪŖ°ė¾¶µÄ”ŃOÉĻŌĖ¶Æ£®ŹżŃ§ŠĖȤŠ”×éĪŖ½ųŅ»²½ŃŠ¾æĘäÖŠĖłŌĢŗ¬µÄŹżŃ§ÖŖŹ¶£¬¹żµćO×÷OH ”ĶlÓŚµćH£¬²¢²āµĆOH = 4·ÖĆ×£¬PQ = 3·ÖĆ×£¬OP = 2·ÖĆ×£®
½ā¾öĪŹĢā
£Ø1£©µćQÓėµćO¼äµÄ×īŠ”¾ąĄėŹĒ ·ÖĆ×£»µćQÓėµćO¼äµÄ×ī“ó¾ąĄėŹĒ ·ÖĆ×£»µćQŌŚlÉĻ»¬µ½×ī×ó¶ĖµÄĪ»ÖĆÓė»¬µ½×īÓŅ¶ĖĪ»ÖĆ¼äµÄ¾ąĄėŹĒ ·ÖĆ×£®
£Ø2£©

ČēĶ¼14-3£¬Š”Ć÷Ķ¬Ń§Ėµ£ŗ”°µ±µćQ»¬¶Æµ½µćHµÄĪ»ÖĆŹ±£¬PQÓė”ŃOŹĒĻąĒŠµÄ£®”±ÄćČĻĪŖĖūµÄÅŠ¶Ļ¶ŌĀš£æĪŖŹ²Ć“£æ
£Ø3£©¢ŁŠ”ĄöĶ¬Ń§·¢ĻÖ£ŗ”°µ±µćPŌĖ¶Æµ½OHÉĻŹ±£¬µćPµ½lµÄ¾ąĄė×īŠ”£®”±ŹĀŹµÉĻ£¬»¹“ęŌŚ×ŵćPµ½l¾ąĄė×ī“óµÄĪ»ÖĆ£¬“ĖŹ±£¬µćPµ½lµÄ¾ąĄėŹĒ ·ÖĆ×£»
¢Śµ±OPČʵćO×óÓŅ°Ś¶ÆŹ±£¬ĖłÉعżµÄĒųÓņĪŖÉČŠĪ£¬ĒóÕāøöÉČŠĪĆ껿×ī“óŹ±Ō²ŠÄ½ĒµÄ¶ČŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬ŅŌABĪŖÖ±¾¶µÄ”ŃO·Ö±šÓŚBC£¬ACĻą½»ÓŚµćD£¬E£¬BD=CD£¬¹żµćD×÷”ŃOµÄĒŠĻß½»±ßACÓŚµćF£®
£Ø1£©ĒóÖ¤£ŗDF”ĶAC£»
£Ø2£©Čō”ŃOµÄ°ė¾¶ĪŖ5£¬”ĻCDF=30”ć£¬![]() Ēó
Ēó![]() ³¤£Ø½į¹ū±£Įō¦Š£©£®
³¤£Ø½į¹ū±£Įō¦Š£©£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ±ß³¤ĪŖaµÄÕż·½ŠĪµÄŅ»½Ē¼õČ„Ņ»øö±ß³¤ĪŖµÄŠ”Õż·½ŠĪ£Øa>b£©£¬ČēĶ¼¢Ł

¢Ł ¢Ś
£Ø1£©ÓÉĶ¼¢ŁµĆŅõÓ°²æ·ÖµÄĆ껿ĪŖ .
£Ø2£©ŃŲĶ¼¢ŁÖŠµÄŠéĻß¼ōæŖĘ“³ÉĶ¼¢Ś£¬ŌņĶ¼¢ŚÖŠŅõÓ°²æ·ÖµÄĆ껿ĪŖ .
£Ø3£©ÓÉ£Ø1£©£Ø2£©µÄ½į¹ūµĆ³ö½įĀŪ£ŗ = .
£Ø4£©ĄūÓĆ£Ø3£©ÖŠµĆ³öµÄ½įĀŪ¼ĘĖć£ŗ20172£20162
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠ²»ŹĒ“śŹżŹ½µÄŹĒ£Ø””””£©
A.£Øx+y£©£Øx©y£©
B.c=0
C.m+n
D.999n+99m
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com