
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①CF=2AF;②tan∠CAD=![]() ;
;
③DF=DC;④△AEF∽△CAB;⑤ S四边形CDEF=![]() S△ABF ,其中正确的结论有( )
S△ABF ,其中正确的结论有( )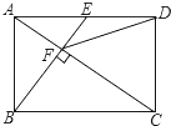
A.2个
B.3个
C.4个
D.5个
【答案】D
【解析】如图:过D作DM∥BE交AC于N,
①∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
∴△AEF∽△CBF,
∴![]() =
=![]() ,
,
又∵E是AD边的中点,
∴AE=![]() AD=
AD=![]() BC,
BC,
∴![]() =
=![]() ,
,
即CF=2AF.
故①正确.
②∵四边形ABCD为矩形,
∴∠ADC=∠ABC=90°,AB=CD,
∴∠DAC+∠ACD=90°,
∴∠BAF=∠ACD,
又∵BE⊥AC,
∴∠AFE=∠ADC=90°,
∴△BAE∽△ADC,
∴![]() =
=![]()
∵AB=CD,AE=![]() AD,
AD,
∴CD=![]() AD,
AD,
∴tan∠CAD=![]() =
=![]() .
.
故②正确.
③∵四边形ABCD为矩形
∴DE∥BM,
∵DM∥BE,
∴四边形BMDE是平行四边形,
∴BM=DE=![]() BC,
BC,
∴BM=CM,
∴CN=FN,
又∵BE⊥AC,DM∥BE,
∴DN⊥CF,
∴DN垂直平分CF,
∴DF=DC,
故③正确.
④∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,∠ABC=90°,
∴∠EAC=∠ACB,
又∵BE⊥AC,
∴∠AFE=∠ABC=90°,
∴△AEF∽△CAB.
故④正确.
⑤∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
∴△AEF∽△CBF,
∴![]() =
=![]() ,
,
又∵E是AD边的中点,
∴AE=![]() AD=
AD=![]() BC,
BC,
∴![]() =
=![]() ,
,
∴S△AEF=![]() S△ABF ,S△AEF=
S△ABF ,S△AEF=![]() S△ABE,S△ABE=
S△ABE,S△ABE=![]() S矩形ABCD,
S矩形ABCD,
∴S△ABF=![]() S矩形ABCD,
S矩形ABCD,
∴S△AEF=![]() S矩形ABCD,
S矩形ABCD,
又∵S四边形CDEF=S△ACD-S△AEF=![]() S矩形ABCD-
S矩形ABCD-![]() S矩形ABCD=
S矩形ABCD=![]() S矩形ABCD,
S矩形ABCD,
∴S四边形CDEF=![]() S△ABF.
S△ABF.
故⑤正确.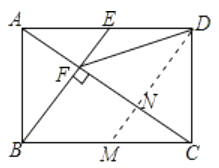
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对平行四边形的判定与性质的理解,了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2 , 交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C2017 . 若点P是第2016段抛物线的顶点,则P点的坐标为 . 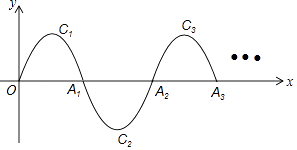
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点 D,E 分别在边 AC,AB 上,BD 与 CE 交于点 O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC 是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=2,BF=8,BC=AE=6,CE=CF=7,则△CDF与四边形ABDE的面积比值是( )
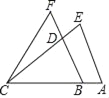
A. 1:1 B. 2:1 C. 1:2 D. 2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象经过点(﹣1,-2
的图象经过点(﹣1,-2![]() ),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当
),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C在第四象限,AC与x轴交于点D,当![]() =
=![]() 时,则点C的坐标为 .
时,则点C的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)写出数轴上点A表示的数;
(2)将长方形OABC沿数轴向右水平移动,移动后的长方形记为![]() ,若移动后的长方形
,若移动后的长方形![]() 与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的
与原长方形OABC重叠部分的面积恰好等于原长方形OABC面积的![]() 时,写出数轴上点
时,写出数轴上点![]() 表示的数;
表示的数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1)、B(﹣3,2)、C(﹣1,4).
①以原点O为位似中心,在第二象限内画出将△ABC放大为原来的2倍后的△A1B1C1 .
②画出△ABC绕C点顺时针旋转90°后得到的△A2B2C.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD于点M.若DG=6,AG=7 ![]() ,则EF的长为 .
,则EF的长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com