
【题目】2017年11月11日,张杰参加了某网点的“翻牌抽奖”活动.如图所示,4张牌上分别写有对应奖品的价值为10元,15元,20元和“谢谢惠顾”的字样.
⑴如果随机翻1张牌,那么抽中有奖的概率为 ,抽中15元及以上奖品的概率为 .
⑵如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,用画树状图或列表法列出抽奖的所有等可能性情况,并求出获奖品总值不低于30元的概率.

【答案】(1)![]() ;
; ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数,据此计算,求出抽中有奖和15元以上奖品的概率为多少即可;
(2)首先应用树状图法,列举出随机翻2张牌,所获奖品的总值一共有多少种情况;然后用所获奖品总值不低于30元的情况的数量除以所有情况的数量,求出所获奖品总值不低于30元的概率为多少即可.
解:(1)3÷4=![]() ,1÷2=
,1÷2=![]() ,
,
∴抽中奖的概率为![]() ,抽中15元及以上的概率为
,抽中15元及以上的概率为![]() ;
;
故答案为: ![]() ;
; ![]() ;
;
(2) 画出树状图得:

∴由树状图可知,一共有12种等可能性的抽奖结果;其中总值不低于30元的有4种情况. 所获奖品总值不低于30元的概率=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块三角形土地,它的底边BC=100米,高AH=80米,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,D、G分别在AB、AC的边上,问当这个矩形面积最大时,它的长与宽各是多少米?面积最大为多少平方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:点B、E、F、C在同一直线上,∠A=∠D,BE=CF,且AB∥CD.求证:AF∥ED
证明:∵BE=FC
∴BE+EF=FC+EF(____________________________)
即:___________
∵AB∥CD
∴∠B=∠C(_________________________)
在△ABF和△DCE中,
∠A=∠D, ∠B=∠C, BF=CE
∴△ABF≌△DCE(________)
∴∠AFB=∠DEC(_________________________________)
∴AF∥ED(__________________________________)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,直线a为对称轴,A和C都在对称轴上.
(1)△ABC以直线a为对称轴作△AB1C;
(2)若∠BAC=30°,则∠BAB1=______°;
(3)求△ABB1的面积等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
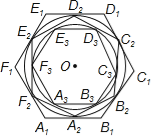
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级有800名学生,在一次跳绳模拟测试中,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:
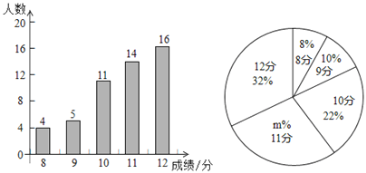
(1)本次抽取到的学生人数为______,扇形统计图中![]() 的值为______.
的值为______.
(2)本次调查获取的样本数据的众数是_____(分),中位数是_____(分).
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
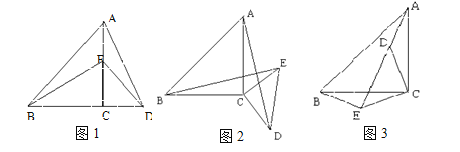
【题目】如图1,E是等腰Rt△ABC边AC上的一个动点(点E与A、C不重合),以CE为一边在Rt△ABC作等腰Rt△CDE,连结AD,BE.我们探究下列图中线段AD,、线段BE 的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的等腰Rt△CDE绕着点C按顺时针方向旋转任意角度![]() ,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
(2)将原题中等腰直角三角形改为直角三角形(如图4—6),且AC=a,BC=b,CD=ka,CE=kb (a![]() b,k
b,k![]() 0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
(3)在第(2)题图5中,连结BD、AE,且a=4,b=3,k=![]() ,求BD2+AE2的值.
,求BD2+AE2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
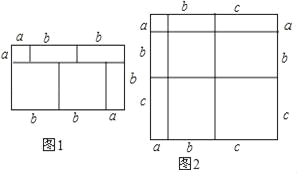
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数字等式,例如图1,可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下问题:
(1)写出图2中所表示的数学等式_____;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=9,ab+bc+ac=26,求a2+b2+c2的值;
(3)小明同学用2张边长为a的正方形、3张边长为b的正方形、5张边长为a、b的长方形纸片拼出了一个长方形,那么该长方形较长一边的边长为多少?
(4)小明同学又用x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出了一个面积为(25a+7b)(2a+5b)长方形,求9x+10y+6.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com