某商场销售甲、乙两种品牌的智能手机，这两种手机的进价和售价如下表所示：
| 甲 | 乙 | |
| 进价（元/部） | 4000 | 2500 |
| 售价（元/部） | 4300 | 3000 |
该商场计划购进两种手机若干部，共需15.5万元，预计
全部销售后获毛利润共2.1万元（毛利润=（售价-进价）×销售量）
（1）该商场计划购进甲、乙两种手机各多少部？
（2）通过市场调研，该商场决定在原计划的基础上，减少甲种手机的购进数量，增加乙种手机的购进数量，已知乙种手机增加的数量是甲种手机减少
的数量的3倍，而且用于购进这两种手机的总资金不超过17.25万元，该商场怎样进货，使全部销售后获得的毛利润最大？并求出最大毛利润。
科目：初中数学 来源： 题型：
对于某一个函数，自变量x在规定的范围内，若任意取两个值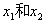
，他们的对应函数值分别为
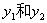。若
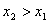时，有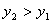
，则称该函数单调递增；若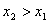时，有
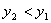，则称该函数单调递减。例如二次函数
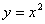，在
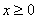时，该函数单调递增；在
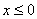时，该函数单调递减。
（1）、二次函数：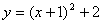
自变量x在哪个范围内，该函数单调递减？答：
（2）、证明：函数：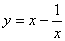
在x>1的函数范围内，该函数单调递增。
（3）、若存在两个关于x的一次函数，分别记为：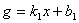
和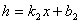
，且函数g在实数范围内单调递增，函数h在实数范围内单调递减。记第三个一次函数
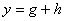，则比例系数
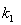和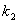
满足何种条件时，函数y在实数范围内单调递增?
查看答案和解析>>
科目：初中数学 来源： 题型：
已知正比例函数y=kx与反比例函数y=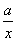
相交于点A(1,b)、点B(c,-2)，求k+a的值。甲同学说：未知数太多，很难求的；乙同学说：可能不是用待定系数法来求；丙说：如果用数形结合的方法，利用两交点在坐标系中位置的特殊性，可以试试。请结合他们的讨论求出k+a=________．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在菱形ABCD中，∠A=110°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠PEF=（ ）
A.35° B.45° C.50° D.55°
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点，若⊙O的半径为9，则GE+FH的最大值为 ．
 |
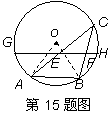查看答案和解析>>
科目：初中数学 来源： 题型：
直角坐标系xoy中，一次函数y=kx+b（kb≠0）的图象过点（1，kb），且b≥2，与x轴、y轴分别交于A、B两点．设△ABO的面积为S，则S的最小值是（ ）
A．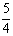
B．1 C．
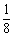D． 不存在
查看答案和解析>>
科目：初中数学 来源： 题型：
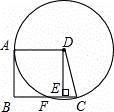
如图，在梯形ABCD中，AD∥BC，DA=DC，以点D为圆心，DA长为半径的⊙D与AB相切于A，与BC交于点F，过点D作DE⊥BC，垂足为E．
（1）求证：四边形ABED为矩形；
（2）若AB=4，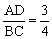
，求CF的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，AB＝5，则边AC的长是（ ） 
C．
D．4