
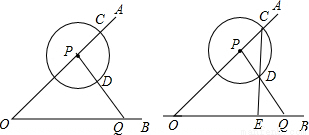 已知∠AOB=45°,P是边OA上一点,OP=4
已知∠AOB=45°,P是边OA上一点,OP=4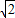 ,以点P为圆心画圆,圆P交OA于点C(点P在O、C之间,如图).点Q是直线OB上的一个动点,连PQ,交圆P于点D,已知,当OQ=7时,
,以点P为圆心画圆,圆P交OA于点C(点P在O、C之间,如图).点Q是直线OB上的一个动点,连PQ,交圆P于点D,已知,当OQ=7时,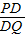 =
= .
.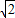 ,根据勾股定理,即求得PG与OG的值,又由OQ=7,
,根据勾股定理,即求得PG与OG的值,又由OQ=7,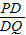 =
= ,即可求得PD的长;
,即可求得PD的长;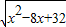 ,然后分别从⊙P与⊙Q外切或外切去分析求解即可求得答案;
,然后分别从⊙P与⊙Q外切或外切去分析求解即可求得答案;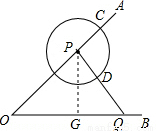 解:(1)过点P作PG⊥OB,垂足为G,
解:(1)过点P作PG⊥OB,垂足为G, ,
,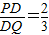 ,
,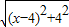 =
=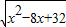 . (1分)
. (1分)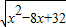 =x+2,…(1分)
=x+2,…(1分) .经检验是方程的根,且符合题意,…(1分)
.经检验是方程的根,且符合题意,…(1分)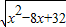 =x-2,…(1分)
=x-2,…(1分) 或7时,⊙P与⊙Q相切.
或7时,⊙P与⊙Q相切.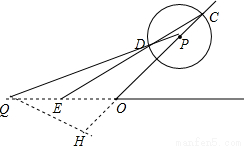
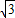 QH,
QH,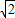 =
=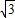 t,
t,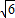 +2
+2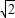 ,
,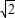 t=4
t=4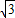 +4.…(2分)
+4.…(2分)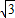 +4时,以O、C、E为顶点的三角形与△OPQ相似.
+4时,以O、C、E为顶点的三角形与△OPQ相似.

科目:初中数学 来源: 题型:
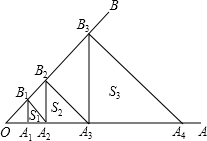 如图,已知∠AOB=45°,A1是OA上的一点,且OA1=1,过A1作OA的垂线交OB于点B1,过点B1作OB的垂线交OA于点A2,过点A2作OA的垂线交OB于点B2…,依次记△A1B1A2,△A2B2A3,△A3B3A4…的面积为S1,S2,S3…,则Sn=
如图,已知∠AOB=45°,A1是OA上的一点,且OA1=1,过A1作OA的垂线交OB于点B1,过点B1作OB的垂线交OA于点A2,过点A2作OA的垂线交OB于点B2…,依次记△A1B1A2,△A2B2A3,△A3B3A4…的面积为S1,S2,S3…,则Sn=查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知∠AOB=45°,P为∠AOB内任一点,且OP=5,请在图中分别画出点P关于OA,OB的对称点P1,P2,连P1O,P2O,P1P2,则△OP1P2的面积为
如图,已知∠AOB=45°,P为∠AOB内任一点,且OP=5,请在图中分别画出点P关于OA,OB的对称点P1,P2,连P1O,P2O,P1P2,则△OP1P2的面积为| 25 |
| 2 |
| 25 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知∠AOB=45°,A1是OA上的一点,OA1=1,过A1作OA的垂线交OB于点B1,过点B1作OB的垂线交OA于点A2;过A2作OA的垂线交OB于点B2…如此继续,依次记△A1B1A2,△A2B2A3,△A3B3A4…的面积为S1,S2,S3…,则S2011=
如图,已知∠AOB=45°,A1是OA上的一点,OA1=1,过A1作OA的垂线交OB于点B1,过点B1作OB的垂线交OA于点A2;过A2作OA的垂线交OB于点B2…如此继续,依次记△A1B1A2,△A2B2A3,△A3B3A4…的面积为S1,S2,S3…,则S2011=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com