
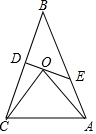
 如图,在△ABC中,∠B=30°,点D是BC的中点,DE⊥BC交AB于点E,点O在DE上,OA=OC,OD=1,OE=2.5,则BE=7,AE=$\frac{9}{2}$.
如图,在△ABC中,∠B=30°,点D是BC的中点,DE⊥BC交AB于点E,点O在DE上,OA=OC,OD=1,OE=2.5,则BE=7,AE=$\frac{9}{2}$. 分析 根据直角三角形的性质得到BE=2DE=2(1+2.5)=7,过O作OF⊥AB于F,根据等腰三角形的性质得到BF=AF,根据直角三角形的性质即可得到结论.
解答 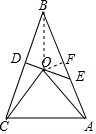 解:∵DE⊥BC,∠B=30°,
解:∵DE⊥BC,∠B=30°,
∴BE=2DE=2(1+2.5)=7,
过O作OF⊥AB于F,
∵点D是BC的中点,
∴OC=OB,
∵OC=OA,
∴OB=OA,
∴BF=AF,
∵∠FEO=60°,
∴EF=$\frac{1}{2}$OE=$\frac{5}{4}$,
∴BF=$\frac{23}{4}$,
∴AF=BF=$\frac{23}{4}$,
∴AE=$\frac{9}{2}$.
故答案为:7,$\frac{9}{2}$.
点评 本题考查了线段垂直平分线的性质,等腰三角形的性质,正确的作出辅助线是解题的关键.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
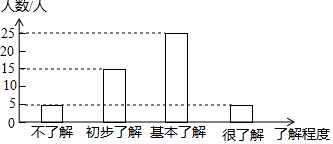 大同中学德育处针对同学们对厦门地铁建设情况的了解程度进行随机抽样调查,并制成如下统计图,请根据图中的信息,解答下列问题:
大同中学德育处针对同学们对厦门地铁建设情况的了解程度进行随机抽样调查,并制成如下统计图,请根据图中的信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com