
”¾ĢāÄæ”æøł¾ŻŹŠĪĄÉś·ĄŅß²æĆŵÄŅŖĒó£¬ÓĪÓ¾³Ų±ŲŠė¶ØĘŚ»»Ė®ŗó²ÅÄܶŌĶāæŖ·Å£®ŌŚ»»Ė®Ź±ŠčŅŖ¾”°ÅÅĖ®”ŖĒåŁž”Ŗ¹ąĖ®”±µÄ¹ż³Ģ£®Ä³ÓĪÓ¾¹Ż“ÓŌēÉĻ7£ŗ00æŖŹ¼¶ŌÓĪÓ¾³Ų½ųŠŠ»»Ė®£¬ŅŃÖŖøĆÓĪÓ¾³ŲµÄÅÅĖ®ĖŁ¶ČŹĒ¹ąĖ®ĖŁ¶ČµÄ1.6±¶£¬ĘäÖŠÓĪÓ¾³ŲÄŚŹ£ÓąµÄĖ®Įæy(m3)Óė»»Ė®Ź±¼äx(h)Ö®¼äµÄŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾£¬øł¾ŻĶ¼Ļó½ā“šĻĀĮŠĪŹĢā£ŗ
(1)ĢīæÕ£ŗøĆÓĪÓ¾³ŲĒåĻ“ŠčŅŖ”” ””Š”Ź±£»
(2)ĒóÅÅĖ®¹ż³ĢÖŠµÄy(m3)Óėx(h)Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮæxµÄȔֵ·¶Ī§£»
(3)ČōøĆÓĪÓ¾¹ŻŌŚ»»Ė®½įŹųŗó30·ÖÖÓ²ÅÄܶŌĶāæŖ·Å£¬ŹŌĪŹÓĪÓ¾°®ŗĆÕߊ”Ć÷ÄÜ·ńŌŚÖŠĪē12£ŗ40½ųČėøĆÓĪÓ¾¹ŻÓĪÓ¾£æ

”¾“š°ø”æ(1)1.2£»(2)ÅÅĖ®¹ż³ĢÖŠµÄyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗy£½£800x+1200(0”Üx”Ü1.5)£»(3)ÓĪÓ¾°®ŗĆÕߊ”Ć÷ÄÜŌŚÖŠĪē12£ŗ40½ųČėøĆÓĪÓ¾¹ŻÓĪÓ¾£®
”¾½āĪö”æ
£Ø1£©øł¾ŻŗÆŹżĶ¼ĻóÖŠµÄŹż¾ŻæÉŅŌ½ā“š±¾Ģā£»
£Ø2£©øł¾ŻĢāŅāŗĖŗÆŹżĶ¼ĻóÖŠµÄŹż¾ŻæÉŅŌĒóµĆÅÅĖ®¹ż³ĢÖŠµÄV£Øm3£©Óėt£Øh£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮætµÄȔֵ·¶Ī§£»
£Ø3£©øł¾ŻĢāŅāæÉŅŌĒóµĆĻĀĪē¼øµćæŖ·Å£¬Č»ŗóÓė13£ŗ30±Č½Ļ“󊔼“æɽā“š±¾Ģā£®
(1)ÓÉĢāŅāæÉµĆ£¬øĆÓĪÓ¾³ŲĒåĻ“ŠčŅŖ£ŗ2.7©1.5£½1.2(Š”Ź±)£¬¹Ź“š°øĪŖ£ŗ1.2£»
(2)ÉčÅÅĖ®¹ż³ĢÖŠµÄy(m3)Óėx(h)Ö®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗy£½kx+b£¬ÓÉĢāÖŖ
![]() £¬½āµĆ
£¬½āµĆ![]() £¬”ąÅÅĖ®¹ż³ĢÖŠµÄyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗ
£¬”ąÅÅĖ®¹ż³ĢÖŠµÄyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗ
y£½£800x+1200(0”Üx”Ü1.5)£»
(3)ÓÉĢāŅāæÉµĆ£¬ÅÅĖ®µÄĖŁ¶ČĪŖ£ŗ1200”Ā1.5£½800(m3/h)£¬
”ą¹ąĖ®µÄĖŁ¶ČĪŖ£ŗ800”Ā1.6£½500(m3/h)£¬”ą¹ąĖ®ÓƵď±¼äĪŖ£ŗ1200”Ā500£½2.4h£¬
”ą¶ŌĶāæŖ·ÅµÄŹ±¼äĪŖ£ŗ7+2.7+2.4+![]() £½12.6£¼12
£½12.6£¼12![]() £¬
£¬
”ąÓĪÓ¾°®ŗĆÕߊ”Ć÷ÄÜŌŚÖŠĪē12£ŗ40½ųČėøĆÓĪÓ¾¹ŻÓĪÓ¾£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗĻ߶ĪAB=40cm.
(1)ČēĶ¼¢Ł£¬µćPŃŲĻ߶ĪAB×ŌµćAĻņµćBŅŌ3ĄåĆ×/ĆėŌĖ¶Æ£¬Ķ¬Ź±µćQĻ߶ĪBA×ŌBµćĻņµćAŅŌ5ĄåĆ×/ĆėŌĖ¶Æ£¬ĪŹ¾¹ż¼øĆėŗóP”¢QĻąÓö£æ
(2)¼øĆėÖÓŗó£¬P”¢QĻą¾ą16ĄåĆ×£æ
(3)ČēĶ¼¢Ś£¬AO=PO=8ĄåĆ×£¬”ĻPOB=40”ć£¬µćPČʵćOŅŌ20¶Č/ĆėµÄĖŁ¶ČĖ³Ź±ÕėŠż×ŖŅ»ÖÜĶ£Ö¹£¬Ķ¬Ź±µćQŃŲÖ±ĻßBA×ŌBµćĻņµćAŌĖ¶Æ£¬¼ŁČōP”¢QĮ½µćÄÜĻąÓö£¬ĒóQŌĖ¶ÆµÄĖŁ¶Č.
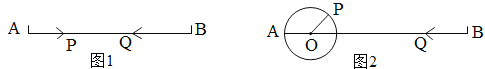
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬A”¢BĮ½µćŌŚŹżÖįÉĻ¶ŌÓ¦µÄŹż·Ö±šĪŖ©12ŗĶ4£®
£Ø1£©Ö±½ÓŠ“³öA”¢BĮ½µćÖ®¼äµÄ¾ąĄė£»
£Ø2£©ČōŌŚŹżÖįÉĻ“ęŌŚŅ»µćP£¬Ź¹µĆAP£½![]() PB£¬ĒóµćP±ķŹ¾µÄŹż£®
PB£¬ĒóµćP±ķŹ¾µÄŹż£®

£Ø3£©ČēĶ¼2£¬ĻÖÓŠ¶ÆµćP”¢Q£¬ČōµćP“ÓµćA³ö·¢£¬ŅŌĆæĆė5øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲŹżÖįĻņÓŅŌĖ¶Æ£¬Ķ¬Ź±µćQ“ÓµćB³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲŹżÖįĻņ×óŌĖ¶Æ£¬µ±µćQµ½“ļŌµćOŗóĮ¢¼“ŅŌĆæĆė3øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲŹżÖįĻņÓŅŌĖ¶Æ£¬Ēó£ŗµ±OP£½4OQŹ±µÄŌĖ¶ÆŹ±¼ätµÄÖµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬Ö±Ļßy=3x+3ÓėxÖį½»ÓŚCµć£¬ÓėyÖį½»ÓŚAµć£¬BµćŌŚxÖįÉĻ£¬”÷OABŹĒµČŃüÖ±½ĒČż½ĒŠĪ£®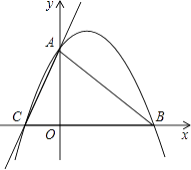
£Ø1£©Ēó¹żA”¢B”¢CČżµćµÄÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ČōÖ±ĻßCD”ĪAB½»Å×ĪļĻßÓŚDµć£¬ĒóDµćµÄ×ų±ź£»
£Ø3£©ČōPµćŹĒÅ×ĪļĻßÉĻµÄ¶Æµć£¬ĒŅŌŚµŚŅ»ĻóĻŽ£¬ÄĒĆ“”÷PABŹĒ·ńÓŠ×ī“óĆ껿£æČōÓŠ£¬Ēó³ö“ĖŹ±PµćµÄ×ų±źŗĶ”÷PABµÄ×ī“óĆ껿£»Čōƻӊ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬¹żµćA×÷AE”ĶBC£¬“¹×ćĪŖE£¬Į¬½ÓDE£¬FĪŖĻ߶ĪDEÉĻŅ»µć£¬ĒŅ”ĻAFE=”ĻB£®
£Ø1£©ĒóÖ¤£ŗ”÷ADF”×”÷DEC£»
£Ø2£©ČōAB=8£¬AD=6 ![]() £¬AF=4
£¬AF=4 ![]() £¬ĒóAEµÄ³¤£®
£¬ĒóAEµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¾ŲŠĪÖ½Ę¬ABCDÖŠ£¬AB=12,BC=16.½«¾ŲŠĪÖ½Ę¬ABCDÕŪµž,Ź¹µćBÓėµćDÖŲŗĻ£¬µćAÕŪµžÖĮµćE“¦£¬GHĪŖÕŪŗŪ£¬Į¬½ÓBG.
(1)”÷DGHŹĒµČŃüČż½ĒŠĪĀš£æĒėĖµĆ÷ÄćµÄĄķÓÉ.
(2)ĒóĻ߶ĪAGµÄ³¤£»
(3)ĒóÕŪŗŪGHµÄ³¤.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĖıߊĪABCDÖŠ£¬AB=AD=8£¬”ĻA=60”ć£¬”ĻD=150”ć£¬ĖıߊĪÖܳ¤ĪŖ32£¬ĒóBCŗĶCDµÄ³¤¶Č£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓĆÖ±³ßŗĶŌ²¹ę»Ņ»øö½ĒµČÓŚŅŃÖŖ½Ē£¬ŹĒŌĖÓĆĮĖ”°Č«µČČż½ĒŠĪµÄ¶ŌÓ¦½ĒĻąµČ”±ÕāŅ»ŠŌÖŹ£¬ĘäČ«µČµÄŅĄ¾ŻŹĒ£Ø £©

A£®SAS B£®ASA C£®AAS D£®SSS
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»ÖÖŹµŃéÓĆ¹ģµĄµÆÖ飬ŌŚ¹ģµĄÉĻŠŠŹ»5·ÖÖÓŗóĄėæŖ¹ģµĄ£¬Ē°2·ÖÖÓĘäĖŁ¶Čv£ØĆ×/·Ö£©ÓėŹ±¼ät£Ø·Ö£©Āś×涞“ĪŗÆŹżv=at2£¬ŗóČż·ÖÖÓĘäĖŁ¶Čv£ØĆ×/·Ö£©ÓėŹ±¼ät£Ø·Ö£©Āś×ć·“±ČĄżŗÆŹż¹ŲĻµ£¬ČēĶ¼£¬¹ģµĄÅŌ±ßµÄ²āĖŁŅĒ²āµĆµÆÖé1·ÖÖÓÄ©µÄĖŁ¶ČĪŖ2Ć×/·Ö£¬Ēó£ŗ
£Ø1£©¶ž“ĪŗÆŹżŗĶ·“±ČĄżŗÆŹżµÄ¹ŲĻµŹ½£®
£Ø2£©µÆÖéŌŚ¹ģµĄÉĻŠŠŹ»µÄ×ī“óĖŁ¶Č£®

”¾“š°ø”æ£Ø1£©v=![]() £Ø2£¼t”Ü5£© £Ø2£©8Ć×/·Ö
£Ø2£¼t”Ü5£© £Ø2£©8Ć×/·Ö
”¾½āĪö”æ·ÖĪö£ŗ£Ø1£©ÓÉĶ¼ĻóæÉÖŖĒ°Ņ»·ÖÖÓ¹żµć£Ø1£¬2£©£¬ŗóČż·ÖÖÓŹ±¹żµć£Ø2£¬8£©£¬·Ö±šĄūÓĆ“ż¶ØĻµŹż·ØæÉĒóµĆŗÆŹż½āĪöŹ½£»
£Ø2£©°Ńt=2“śČė£Ø1£©ÖŠ¶ž“ĪŗÆŹż½āĪöŹ½¼“æÉ£®
Ļź½ā£ŗ£Ø1£©v=at2µÄĶ¼Ļó¾¹żµć£Ø1£¬2£©£¬
”ąa=2£®
”ą¶ž“ĪŗÆŹżµÄ½āĪöŹ½ĪŖ£ŗv=2t2£¬£Ø0”Üt”Ü2£©£»
Éč·“±ČĄżŗÆŹżµÄ½āĪöŹ½ĪŖv=![]() £¬
£¬
ÓÉĢāŅāÖŖ£¬Ķ¼Ļó¾¹żµć£Ø2£¬8£©£¬
”ąk=16£¬
”ą·“±ČĄżŗÆŹżµÄ½āĪöŹ½ĪŖv=![]() £Ø2£¼t”Ü5£©£»
£Ø2£¼t”Ü5£©£»
£Ø2£©”߶ž“ĪŗÆŹżv=2t2£¬£Ø0”Üt”Ü2£©µÄĶ¼ĻóæŖæŚĻņÉĻ£¬¶Ō³ĘÖįĪŖyÖį£¬
”ąµÆÖéŌŚ¹ģµĄÉĻŠŠŹ»µÄ×ī“óĖŁ¶ČŌŚ2ĆėÄ©£¬ĪŖ8Ć×/·Ö£®
µć¾¦£ŗ±¾Ģāæ¼²éĮĖ·“±ČĄżŗÆŹżŗĶ¶ž“ĪŗÆŹżµÄÓ¦ÓĆ£®½āĢāµÄ¹Ų¼üŹĒ“ÓĶ¼ÖŠµĆµ½¹Ų¼üŠŌµÄŠÅĻ¢£ŗ×Ō±äĮæµÄȔֵ·¶Ī§ŗĶĶ¼ĻóĖł¾¹żµÄµćµÄ×ų±ź£®
”¾ĢāŠĶ”æ½ā“šĢā
”¾½įŹų”æ
24
”¾ĢāÄæ”æŌĶĮ²ÄĮĻ£ŗŠ”ÅÖĶ¬Ń§·¢ĻÖÕāŃłŅ»øö¹ęĀÉ£ŗĮ½øö¶„½ĒĻąµČµÄµČŃüČż½ĒŠĪ£¬Čē¹ū¾ßÓŠ¹«¹²µÄ¶„½ĒµÄ¶„µć£¬²¢°ŃĖüĆĒµÄµ×½Ē¶„µćĮ¬½ÓĘšĄ“ŌņŠĪ³ÉŅ»×銿×ŖČ«µČµÄČż½ĒŠĪ£®Š”ÅÖ°Ń¾ßÓŠÕāøö¹ęĀɵÄĶ¼ŠĪ³ĘĪŖ”°ŹÖĄŹÖ”±Ķ¼ŠĪ£®ČēĶ¼1£¬ŌŚ”°ŹÖĄŹÖ”±Ķ¼ŠĪÖŠ£¬Š”ÅÖ·¢ĻÖČō”ĻBAC=”ĻDAE£¬AB=AC£¬AD=AE£¬ŌņBD=CE£®
£Ø1£©ŌŚĶ¼1ÖŠÖ¤Ć÷Š”Åֵķ¢ĻÖ£»
½čÖśŠ”ÅÖĶ¬Ń§×ܽį¹ęĀÉ£¬¹¹Ōģ”°ŹÖĄŹÖ”±Ķ¼ŠĪĄ“½ā“šĻĀĆęµÄĪŹĢā£ŗ
£Ø2£©ČēĶ¼2£¬AB=BC£¬”ĻABC=”ĻBDC=60”ć£¬ĒóÖ¤£ŗAD+CD=BD£»
£Ø3£©ČēĶ¼3£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬”ĻBAC=m”ć£¬µćEĪŖ”÷ABCĶāŅ»µć£¬µćDĪŖBCÖŠµć£¬”ĻEBC=”ĻACF£¬ED”ĶFD£¬Ēó”ĻEAFµÄ¶ČŹż£ØÓĆŗ¬ÓŠmµÄŹ½×Ó±ķŹ¾£©£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com