
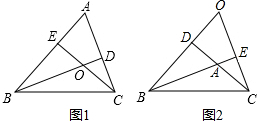
 (1)已知如图1,锐角△ABC中,AB、AC边上的高CE、BD相交于O点.若∠A=70°,则∠BOC=110°.
(1)已知如图1,锐角△ABC中,AB、AC边上的高CE、BD相交于O点.若∠A=70°,则∠BOC=110°.分析 (1)根据垂直的定义得到∠ADB=90°,根据三角形内角和定理求出∠ABD,根据三角形的外角的性质解答;
(2)仿照(1)的做法,代入计算即可.
解答 解:(1)∵BD⊥AC,
∴∠ADB=90°,
∴∠ABD+∠A=90°,
∴∠ABD=90°-70°=20°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠BOC=∠BEC+∠ABD=110°,
故答案为:=110°;
(2))∵BD⊥AC,
∴∠ADB=90°,
∴∠ABD+∠A=90°,
∴∠ABD=90°-n°,
∵CE⊥AB,
∴∠BEC=90°,
∴∠BOC=∠BEC+∠ABD=(180-n)°.
点评 本题考查的是三角形内角和定理,掌握三角形内角和等于180°是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com