
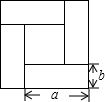
 如图是由四个大小一样的纸片围成的图形,利用面积的不同表示方法,写出一个代数恒等式
如图是由四个大小一样的纸片围成的图形,利用面积的不同表示方法,写出一个代数恒等式科目:初中数学 来源: 题型:
 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径;查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(安徽芜湖卷)数学(带解析) 题型:解答题
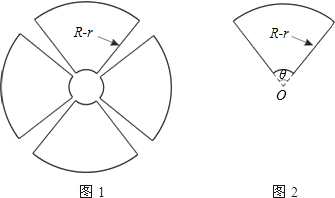
一园林设计师要使用长度为4L的材料建造如图1所示的花圃,该花圃是由四个形状、大小完全一样的扇环面组成,每个扇环面如图2所示,它是以点O为圆心的两个同心圆弧和延长后通过O点的两条直线段围成,为使得绿化效果最佳,还须使得扇环面积最大.
(1)求使图1花圃面积为最大时R-r的值及此时花圃面积,其中R、r分别为大圆和小圆的半径;
(2)若L=160m,r=10m,求使图2面积为最大时的θ值.
查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(安徽芜湖卷)数学(解析版) 题型:解答题
一园林设计师要使用长度为4L的材料建造如图1所示的花圃,该花圃是由四个形状、大小完全一样的扇环面组成,每个扇环面如图2所示,它是以点O为圆心的两个同心圆弧和延长后通过O点的两条直线段围成,为使得绿化效果最佳,还须使得扇环面积最大.

(1)求使图1花圃面积为最大时R-r的值及此时花圃面积,其中R、r分别为大圆和小圆的半径;
(2)若L=160m,r=10m,求使图2面积为最大时的θ值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com