
【题目】如图,已知抛物线y=﹣ ![]() +bx+c图象经过A(﹣1,0),B(4,0)两点.
+bx+c图象经过A(﹣1,0),B(4,0)两点.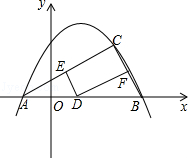
(1)求抛物线的解析式;
(2)若C(m,m﹣1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②试探究:在点D运动过程中,DE、DF、CF的长度之和是否发生变化?若不变,求出它的值,若变化,试说明变化情况.
【答案】
(1)
解:因为抛物线与x轴交于(﹣1,0)(4,0),可以假设y=a(x+1)(x﹣4)
∵a=﹣ ![]() ,
,
∴y=﹣ ![]() (x+1)(x﹣4)
(x+1)(x﹣4)
即y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:①证明:把C(m,m﹣1)代入y=﹣ ![]() x2+
x2+ ![]() x+2得
x+2得
m﹣1=﹣ ![]() m2+
m2+ ![]() m+2,
m+2,
∴m1=﹣2,m2=3,
∵C在第一象限,
∴ ![]() ,∴m>1,
,∴m>1,
∴m=﹣2(不符合题意,舍),m=3,
∴C的坐标是(3,2),
∵BC∥DE DF∥AC,
∴四边形DECF是平行四边形,
∵AB2=25 AC2=20 BC2=5
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴四边形BECF是矩形.
②∵DE∥BC,
∴△AED∽△ACB,
∴ ![]() =
= ![]() (1).
(1).
同理,得
![]() =
= ![]() (2),
(2),
⑴+(2)得
![]() +
+ ![]() =
= ![]() =1,
=1,
∵AC=2 ![]() ,BC=
,BC= ![]() ,CF=ED,
,CF=ED,
∴ ![]() +
+ ![]() =1,
=1,
即2ED+DF=2 ![]() ,
,
∴ED+DF+FC=2 ![]() ,
,
∴DE、DF、CF的长度之和不变化,ED+DF+FC=2 ![]()
![]() 代入整理即可求出b、c.(2)①利用待定系数法思想求出点C坐标,利用勾股定理的逆定理证明∠ACB=90°,由此即可解决问题;②根据相似三角形的判定与性质,可得
代入整理即可求出b、c.(2)①利用待定系数法思想求出点C坐标,利用勾股定理的逆定理证明∠ACB=90°,由此即可解决问题;②根据相似三角形的判定与性质,可得 ![]() =
= ![]() ,
, ![]() =
= ![]() ,根据等式的性质,可得
,根据等式的性质,可得 ![]() +
+ ![]() ,再根据等量代换,可得答案.
,再根据等量代换,可得答案.
【考点精析】关于本题考查的勾股定理的概念和相似三角形的判定与性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】某文具零售店准备从批发市场选购A、B两种文具,批发价A种为12元/件,B种为8元/件.若该店零售A、B两种文具的日销售量y(件)与零售价x(元/件)均成一次函数关系.(如图) 
(1)求y与x的函数关系式;
(2)该店计划这次选购A、B两种文具的数量共100件,所花资金不超过1000元,并希望全部售完获利不低于296元,若按A种文具每件可获利4元和B种文具每件可获利2元计算,则该店这次有哪几种进货方案?
(3)若A种文具的零售价比B种文具的零售价高2元/件,求两种文具每天的销售利润W(元)与A种文具零售价x(元/件)之间的函数关系式,并说明A、B两种文具零售价分别为多少时,每天销售的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图: 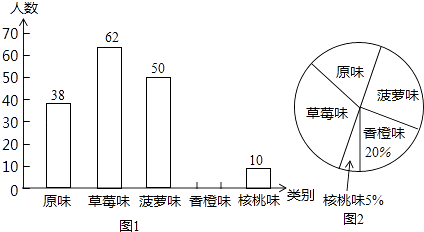
(1)本次被调查的学生有名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便居民低碳出行,聊城市公共自行车租赁系统(一期)试运行.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°. 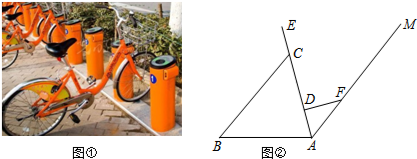
(1)求AD的长;
(2)求点E到AB的距离.(精确到0.1cm,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x= ![]() ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a﹣b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a﹣b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( ) 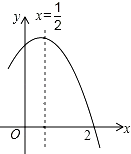
A.①②③④
B.③④
C.①③④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系 xOy 中,A(2,3),B(3,1),C(﹣2,﹣1).
①在图中作出△ABC 关于 x 轴的对称图形△A1B1C1 并写出 A1,B1,C1 的坐标;
②在 y 轴上画出点 P,使 PA+PB 最小.(不写作法,保留作图痕迹)
③求△ABC 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com