
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A',点B、C的对应点分别是点B'、C'.
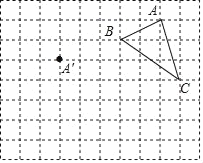
(1)△ABC的面积是 ;
(2)画出平移后的△A'B'C';
(3)若连接AA'、CC′,这两条线段的关系是 .
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
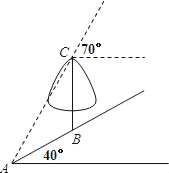
【题目】如图,在一个坡角为40°的斜坡上有一棵树BC,树高4米.当太阳光AC与水平线成70°角时,该树在斜坡上的树影恰好为线段AB,求树影AB的长.(结果保留一位小数)
(参考数据:sin20°=0.34,tan20°=0.36,sin30°=0.50,tan30°=0.58,sin40°=0.64,tan40°=0.84,sin70°=0.94,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD分别平分△ABC的外角∠EAC、内角∠ABC,以下结论:① AD∥BC;②∠ACB=2∠ADB;③ BD⊥AC;④ AC=AD.其中正确的结论有( )

A.①②B.①②④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某县政府部门决定,招标一工程队负责完成一座水库的土方施工任务.该工程队有A,B两种型号的挖掘机,已知1台A型和2台B型挖掘机同时施工1小时共挖土80立方米,2台A型和3台B型挖掘机同时施工1小时共挖土140立方米.每台A型挖掘机一个小时的施工费用是350元,每台B型挖掘机一个小时的施工费用是200元.
(1)分别求每台A型,B型挖掘机一小时各挖土多少立方米?
(2)若A型和B型挖掘机共10台同时施工4小时,至少完成1360立方米的挖土量,且总费用不超过14000元.问施工时有哪几种调配方案?且指出哪种调配方案的施工费用最低,最低费用多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某汽车行驶的路程S(千米)与时间t(分)的函数关系图.观察图中所提供的信息,解答下列问题:
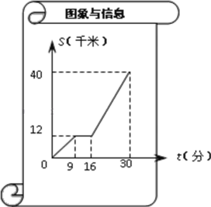
(1)汽车在前9分钟内的平均速度是______千米/分;
(2)当16≤t≤30时,求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147 000元,已知甲、乙、丙三种型号的电视机的出厂价格分别为1 000元/台,1 500元/台,2 000元/台.
(1)求该商场至少购买丙种电视机多少台?
(2)若要求甲种电视机的台数不超过乙种电视机的台数,问有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,设点P(x1,y1),Q(x2,y2)是图形W上的任意两点. 定义图形W的测度面积:若|x1-x2|的最大值为m,|y1-y2|的最大值为n,则S=mn为图形W的测度面积. 例如,若图形W是半径为l的⊙O. 当P,Q分别是⊙O与x轴的交点时,如图1,|x1-x2|取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,|y1-y2|取得最大值,且最大值n=2. 则图形W的测度而积S=mn=4.

(1)若图形W是抛物线y=-x2+2x+3和直线y=2x-1围成的封闭图形,则它的测度面积S=______

(2)若图形W是一个边长为1的正方形ABCD.
①当A,B两点均在x轴上时,它的测度面积S=_________;
②此图形测度面积S的最大值为_________;
(3)若图形W是一个边长分别为3和6的矩形ABCD,求它的测度面积S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“三节三爱”号召,我校把用电习惯分为“很注意节约用电(![]() )”、“较注意节约用电(
)”、“较注意节约用电(![]() )”“不注意节约用电(
)”“不注意节约用电(![]() )”三类情况,设计了调查问卷在中学生中开展调查,并将调查结果分析整理后,制成如图所示的两个统计图.
)”三类情况,设计了调查问卷在中学生中开展调查,并将调查结果分析整理后,制成如图所示的两个统计图.

请根据以上信息解答下列问题:
(1)这次问卷调查共调查了多少名学生?其中“较注意节约用水”的学生有多少人?
(2)在扇形统计图中,“![]() ”所对应的扇形的圆心角度数是多少?
”所对应的扇形的圆心角度数是多少?
(3)如果设该校共有学生![]() 人,试估计“不注意节约用电”的学生人数.
人,试估计“不注意节约用电”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A点坐标是(0,6),M点坐标是(8,0).P是射线AM上一点,PB⊥x轴,垂足为B.设AP=a.
(1)AM= ;
(2)如图,以AP为直径作圆,圆心为点C.若⊙C与x轴相切,求a的值;
(3)D是x轴上一点,连接AD、PD.若△OAD∽△BDP,试探究满足条件的点D的个数(直接写出点D的个数及相应a的取值范围,不必说明理由).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com