
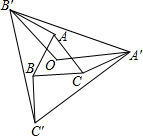
 如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB′、BC′、CA′,连接A′B′、B′C′、A′C′、OA′、OB′.
如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB′、BC′、CA′,连接A′B′、B′C′、A′C′、OA′、OB′.分析 (1)△A'B'C'是等边三角形,根据中心角的定义求解;
(2)当O,A,B'三点在一条直线上时,B'在OA的延长线上时,OB'最大,A′B′C′边长最大,则△A′B′C′的周长最大.
解答 解:(1)∠A′OB′=$\frac{360°}{3}$=120°,
故答案是:120;
(2)△A'B'C'是等边三角形,△A′B′C′的周长最大,则边长最大,则OB'最大,当O,A,B'三点在一条直线上时,B'在OA的延长线上,OB'最大.
∠BAO=$\frac{1}{2}$∠BAC=30°,
则a=180°-30°=150°.
故答案是:150.
点评 本题考查了三角形的旋转,正确理解△A′B′C′的周长最大的条件是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
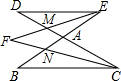 如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.
如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线,EF与CD交于点M,CF与BE交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.475×1010 | B. | 5.475×107 | C. | 5.475×106 | D. | 5475×103 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com