
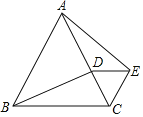
【题目】如图,△ABC是等边三角形,点D在AC边上,将△BCD绕点C旋转得到△ACE.
(1)求证:DE∥BC.
(2)若AB=8,BD=7,求△ADE的周长.
【答案】(1)见解析;(2)15
【解析】
(1)由旋转的性质可得CD=CE,∠ACB=∠ACE=60°,可得∠CDE=60°=∠ACB,可证DE∥BC;
(2)由旋转的性质可得AE=BD=7,即可求△ADE的周长.
证明:(1)∵△ABC是等边三角形,
∴AB=BC=AC,∠ACB=60°,
∵将△BCD绕点C旋转得到△ACE.
∴CD=CE,∠ACB=∠ACE=60°,
∴△CDE是等边三角形,
∴∠CDE=60°=∠ACB,
∴DE∥BC;
(2)∵将△BCD绕点C旋转得到△ACE.
∴AE=BD=7,
∵△ADE的周长=AE+DE+AD=AE+DC+AD=AE+AC,
∴△ADE的周长=7+8=15.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=90°,已知AB=3,BC=4,点Q是线段AC上的一个动点,过点Q作AC的垂线交直线AB于点P,当△PQB为等腰三角形时,线段AP的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,∠BAC=120°,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
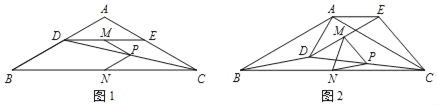
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,∠MPN的度数是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=8,请直接写出△PMN面积的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学解一元二次方程x2﹣6x﹣1=0的过程如图所示.
解:x2﹣6x=1 …①
x2﹣6x+9=1 …②
(x﹣3)2=1 …③
x﹣3=±1 …④
x1=4,x2=2 …⑤
(1)小明解方程的方法是 .
(A)直接开平方法 (B)因式分解法 (C)配方法 (D)公式法
他的求解过程从第 步开始出现错误.
(2)解这个方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,沿射线
同时出发,沿射线![]() 、线段
、线段![]() 向点
向点![]() 的方向运动(点
的方向运动(点![]() 可运动到
可运动到![]() 的延长线上),当动点
的延长线上),当动点![]() 运动到点
运动到点![]() 时,
时,![]() 、
、![]() 两点同时停止运动.联结
两点同时停止运动.联结![]() 、
、![]() 、
、![]() ,过
,过![]() 三边的中点作
三边的中点作![]() .设动点
.设动点![]() 、
、![]() 的速度都是1个单位/秒,
的速度都是1个单位/秒,![]() 、
、![]() 运动的时间为
运动的时间为![]() 秒.试解答下列问题:
秒.试解答下列问题:
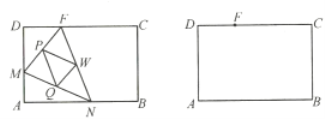
(1)说明![]() ;
;
(2)设![]() ,试问
,试问![]() 为何值时,
为何值时,![]() 为直角三角形?
为直角三角形?
(3)试用含![]() 的代数式表示
的代数式表示![]() ,并求当
,并求当![]() 为何值时,
为何值时,![]() 最小?求此时
最小?求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
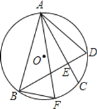
【题目】如图,半径为R的⊙O的弦AC=BD,AC、BD交于E,F为![]() 上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=
上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=![]() R;③在②的条件下,若
R;③在②的条件下,若![]() ,AB=
,AB=![]() ,则BF+CE=1.其中正确的是( )
,则BF+CE=1.其中正确的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果超市以每千克6元的价格购进了一批水果,经测算,此水果超市每天需支出固定费用(包括房租,水电费,员工工资等)为600元.若该种水果的销售单价不超过10元,则日销售量为300千克;若该种水果的销售单价超过10元,则每超过1元,日销售就减少12千克.设该种水果的销售单价为x(x>6,且x为整数)元,日净收入为y元(日净收入=日销售利润﹣每天固定支出的费用).
(1)求y与x之间的函数关系式;
(2)此水果超市销售该种水果的日净收入能否达到1560元?否能,请求出此时的销售单价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com