
分析 (1)利用二次函数的对称轴的公式,和图象上点满足抛物线解析式,列方程求解即可;
(2)利用求两个函数图象的交点坐标是联立方程组求解,根据n=x1+x2-2求出m,n的函数关系式,再由点P,Q的坐标即可;
(3)根据△ABC的面积的两种求法,建立方程即可.
解答 解:(1)∵抛物线y=ax2+bx-3a经过点(0,3),
∴-3a=3,
∴a=-1
∵抛物线y=ax2+bx-3a的对称轴为直线x=1,
∴-$\frac{b}{2a}$=1,
∴b=2,
即:a=-1,b=2;
(2)由(1)有,a=-1,b=1,
∴抛物线y=-x2+2x+3,
∵抛物线与直线y=-$\frac{1}{m}$(x-3)(m≠0)两交点的横坐标为x1,x2,
∴-x2+2x+3=-$\frac{1}{m}$(x-3),
∴x1=3,x2=$\frac{1}{m}$-1,
∵n=x1+x2-2,
∴n=3+$\frac{1}{m}$-1-2=$\frac{1}{m}$,
∵P(1,y0),Q(x0,$\frac{1}{2}$)两点在动点M(m,n)所形成的曲线上,
∴y0=1,x0=2,
∴P(1,1),Q(2,$\frac{1}{2}$),
∴直线PQ的解析式为y=-$\frac{1}{2}$x+$\frac{3}{2}$;
(3)∵抛物线y=-x2+2x+3与x轴交于A,B两点,
∴A(-1,0),B(3,0),
设点C(c,d),
∴AB=4,AC=$\sqrt{(c+1)^{2}+{d}^{2}}$,BC=$\sqrt{(c-3)^{2}+{d}^{2}}$,
∴S△ABC=$\frac{1}{2}$AB×|yc|=$\frac{1}{2}$×4×|d|=2|d|,
S△ABC=$\frac{1}{2}$AC×BCsin∠ACB=$\frac{1}{2}$$\sqrt{(c+1)^{2}+{d}^{2}}$×$\sqrt{(c-3)^{2}+{d}^{2}}$×$\frac{\sqrt{2}}{2}$,
∴2|d|=$\frac{1}{2}$$\sqrt{(c+1)^{2}+{d}^{2}}$×$\sqrt{(c-3)^{2}+{d}^{2}}$×$\frac{\sqrt{2}}{4}$①,
∵点C在抛物线y=-x2+2x+3上,
∴d=-c2+2c+3②
①②联立解得,d=0(舍)或d=-3,
∴c=1±$\sqrt{7}$,
∴C(1-$\sqrt{7}$,-3)或C(1+$\sqrt{7}$,-3)
点评 此题是二次函数综合题,主要考查了二次函数的对称轴的公式,二次函数的性质,待定系数法求函数解析式,三角形的面积的计算方法,求图象的交点坐标是解本题的关键.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
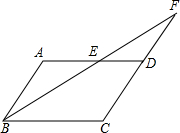 如图,在?ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长是( )
如图,在?ABCD中,AB=4,AD=7,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF的长是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
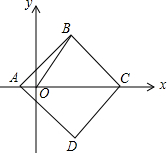 如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )
如图,在平面直角坐标系中,O为坐标原点,正方形ABCD的对角线AC落在x轴上,A(-1,0),C(7,0),连接OB,则∠BOC的正弦值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD的对角线AC、BD相交于点0,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为6,则cos∠BOE=$\frac{2}{3}$.
如图,矩形ABCD的对角线AC、BD相交于点0,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为6,则cos∠BOE=$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
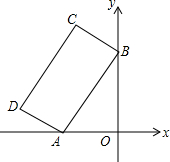 如图,矩形ABCD的两个顶点A,B在坐标轴上,AD:AB=1:2,且A(-2,0),∠BAO=60°,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过该矩形的顶点,则k=-2-$\sqrt{3}$或-6-$\sqrt{3}$.
如图,矩形ABCD的两个顶点A,B在坐标轴上,AD:AB=1:2,且A(-2,0),∠BAO=60°,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过该矩形的顶点,则k=-2-$\sqrt{3}$或-6-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
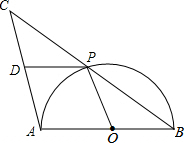 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
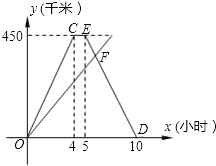 A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.
A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com