
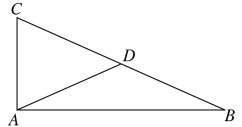
【题目】如图,在Rt△ABC中,∠BAC=90°,点D为BC中点,将△ABD绕点A按逆时针方向旋转50°,记点D在旋转过程中所经过的路径长为m,将△ABD绕点C按顺时针方向旋转100°,则点D在旋转过程中所经过的路径长为________.(用含m的代数式表示)
 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
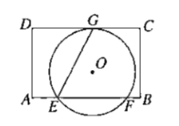
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上一点,且
上一点,且![]() .已知
.已知![]() 经过点
经过点![]() ,与边
,与边![]() 所在直线相切于点
所在直线相切于点![]() (
(![]() 为锐角),与边
为锐角),与边![]() 所在直线交于另一点
所在直线交于另一点![]() ,且
,且![]() ,当边
,当边![]() 或
或![]() 所在的直线与
所在的直线与![]() 相切时,
相切时,![]() 的长是( )
的长是( )
A.1或3B.4或![]() C.
C.![]() 或
或![]() D.4或12
D.4或12
查看答案和解析>>
科目:初中数学 来源: 题型:
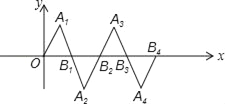
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
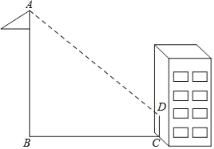
【题目】数学兴趣小组的同学们,想利用自己所学的数学知识测量学校旗杆的高度:下午活动时间,兴趣小组的同学们来到操场,发现旗杆的影子有一部分落在了墙上(如图所示).同学们按照以下步骤进行测量:测得小明的身高1.65米,此时其影长为2.5米;在同一时刻测量旗杆影子落在地面上的影长BC为9米,留在墙上的影高CD为2米,请你帮助兴趣小组的同学们计算旗杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲乙两地同时销售某种品牌的汽车,已知在甲地的总销售利润y(单位:万元)与销售量x(单位:辆)之间满足y=﹣![]() x2+10x,在乙地每销售一辆汽车可获得2万元的销售利润,若该公司在甲乙两地共销售30辆该品牌的汽车,甲乙两地总的销售利润为W万元,其中在甲地销售x辆.
x2+10x,在乙地每销售一辆汽车可获得2万元的销售利润,若该公司在甲乙两地共销售30辆该品牌的汽车,甲乙两地总的销售利润为W万元,其中在甲地销售x辆.
(1)求W与x的函数关系式;
(2)甲乙两地各销售多少辆车时W最大?W的最大值是多少?
(3)为了开拓甲地市场,公司规定甲地平均每辆汽车的销售利润不高于2万元,那么公司销售这30辆汽车可获得的最大销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋时节,硕果飘香,某精准扶贫项目果园上市一种有机生态水果,为帮助果园拓宽销路.欣欣超市对这种水果进行代销,进价为5元/千克,售价为6元/千克时,当天的销售量为60千克;在销售过程中发现:销售单价每上涨0.5元,当天的销售量就减少5千克.设当天销售单价统一为x元/千克(x≥6,且x按0.5元的倍数上涨),当天销售利润为y元.
(1)求y与x的函数关系式;
(2)若该种水果每千克的利润不超过80%,求当天获得利润的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
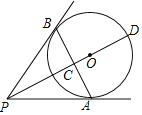
A. PA=PBB. ∠BPD=∠APDC. AB⊥PDD. AB平分PD
查看答案和解析>>
科目:初中数学 来源: 题型:
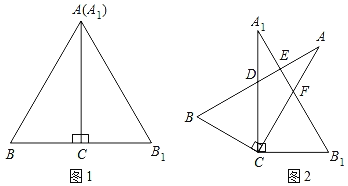
【题目】将两块全等的含30°角的直角三角板按如图1所示的方式放置,已知∠BAC=∠B1A1C=30°.固定三角板A1B1C,然后将三角板ABC绕直角顶点C顺时针旋转(旋转角小于90°)至如图2所示的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
(1)当旋转角等于20°时,∠BCB1= °;
(2)当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个实数根x1,x2.
有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得![]() 成立?若存在,请求出k的值;若不存在,请说明理由.
成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com