
����Ŀ����ѧ��Ȥ����ϣ�С�½�����![]() �ĵױ�
�ĵױ�![]() ��ֱ��
��ֱ��![]() �غϣ�
�غϣ�
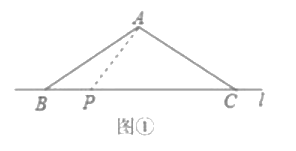
��1����ͼ![]() ����
����![]() ��
��![]() ����
����![]() �ڱ�
�ڱ�![]() ���ڵ�ֱ��
���ڵ�ֱ��![]() ���ƶ������ݡ�ֱ����һ�㵽ֱ�������е�������д��߶���̡���С�·���
���ƶ������ݡ�ֱ����һ�㵽ֱ�������е�������д��߶���̡���С�·���![]() ����Сֵ��____________��
����Сֵ��____________��
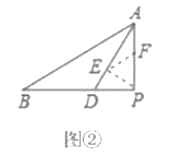
��2��Ϊ��һ�����øý��ۣ��ڣ�1���������£�С�·��֣���![]() ���ʱ����ͼ
���ʱ����ͼ![]() ����
����![]() ����
�У���![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() С�³���̽��
С�³���̽��![]() ����Сֵ��С����
����Сֵ��С����![]() �Ͻ�ȡ
�Ͻ�ȡ![]() ʹ��
ʹ��![]() ����
����![]() ��֤
��֤![]() ���Ӷ���
���Ӷ���![]() ת��Ϊ
ת��Ϊ![]() ת������1�����������
ת������1�����������![]() ����СֵΪ����������
����СֵΪ����������
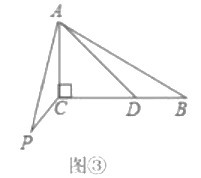
��3��������⣺��ͼ![]() ����
����![]() ��
��![]() ����
����![]() �DZ�
�DZ�![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() ���߶�
���߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ���õ��߶�
���õ��߶�![]() ����
����![]() �����߶�
�����߶�![]() ����Сֵ��
����Сֵ��
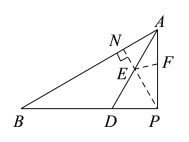
���𰸡���1��2����2��![]() ����3��3��
����3��3��
��������
��1�����ݵ��������ε�������⼴�ɣ�
��2������С�µ�˼·���ѽ�![]() ת��Ϊ
ת��Ϊ![]() ��P��E��N���㹲����
��P��E��N���㹲����![]() ʱ
ʱ![]() ��ֵ��С��
��ֵ��С��
��3����![]() ��ȡһ��
��ȡһ��![]() ��ʹ��
��ʹ��![]() ������
������![]() ��
��![]() ����
����![]() ���Ƴ�
���Ƴ�![]() ����֪
����֪![]() ʱ��
ʱ��![]() ��ֵ��С�����
��ֵ��С�����![]() ����Сֵ���ɽ�����⣮
����Сֵ���ɽ�����⣮
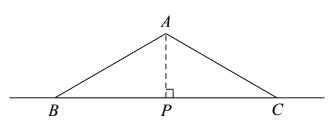
��1����ͼ������A��![]() ����ʱAP��ֵ��С��
����ʱAP��ֵ��С��
��![]() ��
��
![]() ��
��
![]() ��
��
�ʴ�Ϊ��2��
��2������С�µ�˼·����ͼ�Σ���֪��![]() ʱ
ʱ![]() ��ֵ��С����ͼ��
��ֵ��С����ͼ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��
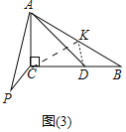
��3����ͼ3�У���![]() ��ȡһ��
��ȡһ��![]() ��ʹ��
��ʹ��![]() ������
������![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ʱ��
ʱ��![]() ��ֵ��С����СֵΪ3��
��ֵ��С����СֵΪ3��
![]() ����СֵΪ3��
����СֵΪ3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x�Ķ��κ���y��ax2��2ax��a��0���Ķ���ΪC����x�ύ�ڵ�O��A������x��һ�κ���y����ax��a��0����
��1����˵����C��һ�κ�����ͼ���ϣ�
��2���������㣨k��y1������k+2��y2����k��0����2�����ڶ��κ�����ͼ���ϣ��Ƿ��������k������![]() ��������ڣ������k��ֵ����������ڣ���˵�����ɣ�
��������ڣ������k��ֵ����������ڣ���˵�����ɣ�
��3������E�Ƕ��κ���ͼ����һ���㣬E��ĺ�������n���ҩ�1��n��1������E��y���ƽ���ߣ���һ�κ���ͼ���ڵ�F����0��a��2ʱ�����߶�EF�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017����A����11�⣩��ͼ��С���ڳ�����ij�t��̨D������ý����ϵ��洬A�ĸ���Ϊ40������DE=3�ף�CE=2�ף�CEƽ���ڽ���AB��ӭˮ��BC���¶�i=1��0.75���³�BC=10�ף����ʱAB�ij�ԼΪ�����������ο����ݣ�sin40���0.64��cos40���0.77��tan40���0.84����

A. 5.1�� B. 6.3�� C. 7.1�� D. 9.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
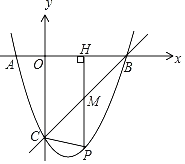
����Ŀ����ͼ����������y��x2+bx+c��x���ཻ��A��B���㣬��y���ཻ�ڵ�C��ֱ��y��x��3������B��C��
��1���������ߵĽ���ʽ��
��2����P��ֱ��BC�·���������һ���㣬����P��PH��x���ڵ�H����BC�ڵ�M������PC��
���߶�PM�Ƿ������ֵ������У�������ֵ�����û�У���˵�����ɣ�
���ڵ�P�˶��Ĺ����У��Ƿ���ڵ�M��ǡ��ʹ��PCM����PMΪ���ĵ��������Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ǰ�����ջ�ɽ���µ�С��ׯ�ļ���������ɽ�˺����������ڰ�����������Ϸ��ֻ��������һ����ɫ�Ĵ�������װ��С����״��������ȫ��ͬ�İ���20ֻ����ÿһ�����϶�д�к���(1~20��)��1ֻ�������涨:ÿ��ֻ��һֻ��.��ǰ��1ԪǮ����1~20��дһ����������������5Ԫ����������������д�ĺ�����ͬ��10Ԫ.
(1)����Ϊ����Ϸ������������������?˵���������.
(2)��һ�����������߶������������ƽ��ÿ�ν���������ʧ����Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ���ѧ�ľ���������������һ�����⣺�����лƽ��ö������һʮһö����֮���ʵȣ�������һ������ʮ�������ʽ������ؼ��Σ�����˼�ǣ��״���װ�лƽ�9ö��ÿö�ƽ�������ͬ�����Ҵ���װ�а���11ö��ÿö����������ͬ��������������ȣ��������ཻ��1ö�״����Ҵ�����13���������������Բ��ƣ����ʻƽ𡢰���ÿö���ض�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx��b��ͼ���뷴��������y��![]() ��ͼ���ཻ��A(-1��n)��B(2��-1)���㣬��y���ཻ�ڵ�C��
��ͼ���ཻ��A(-1��n)��B(2��-1)���㣬��y���ཻ�ڵ�C��
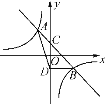
��1����һ�κ����뷴���������ı���ʽ��
��2������D���C����x��Գƣ�����ABD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
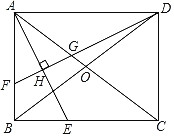
����Ŀ��������̽����
��ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AEƽ�֡�BAC����BC�ڵ�E����DF��AE�ڵ�H���ֱ�AB��AC�ڵ�F��G��
��1���жϡ�AFG����״��˵�����ɣ�
��2����֤��BF=2OG��
��Ǩ��Ӧ�ã�
��3���ǡ�DGO�����ΪS1����DBF�����ΪS2����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
����չ���죩
��4����DF������AB�ڵ�F��������̽�����е������������䣬����EF������BEF�����Ϊ����ABCD�����![]() ʱ����ֱ��д��tan��BAE��ֵ��
ʱ����ֱ��д��tan��BAE��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�Ķ��κ���![]() ��kΪ��������һ�κ���
��kΪ��������һ�κ���![]() ��
��
��1����֤������![]() ��ͼ����x���н��㣮
��ͼ����x���н��㣮
��2����֪����![]() ��ͼ����x������������ľ������3��
��ͼ����x������������ľ������3��
�������ʱk��ֵ��
����![]() ������x��ȡֵ��Χ��
������x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com