
【题目】已知抛物线![]() (m为常数,﹣1≤m≤4).A(﹣m﹣1,
(m为常数,﹣1≤m≤4).A(﹣m﹣1,![]() ),B(
),B(![]() ,
,![]() ),C(﹣m,
),C(﹣m,![]() )是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
(1)用含m的代数式表示抛物线的顶点坐标;
(2)若无论m取何值,抛物线与直线y=x﹣km(k为常数)有且仅有一个公共点,求k的值;
(3)当1<PH≤6时,试比较![]() ,
,![]() ,
,![]() 之间的大小.
之间的大小.
【答案】(1)顶点坐标(![]() ,
,![]() );(2)k=3;(3)﹣1≤m<
);(2)k=3;(3)﹣1≤m<![]() 或
或![]() <m≤
<m≤![]() 时,有
时,有![]() ,
,![]() <m<
<m<![]() 时,有
时,有![]() .
.
【解析】
试题分析:(1)根据顶点坐标公式即可解决问题.
(2)列方程组根据△=0解决问题.
(3)首先证明![]() ,再根据点B的位置,分类讨论,①令
,再根据点B的位置,分类讨论,①令![]() <﹣m﹣1,求出m的范围即可判断,②令
<﹣m﹣1,求出m的范围即可判断,②令![]() =﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
=﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
③令![]() >﹣m﹣1,求出m的范围即可判断,④令
>﹣m﹣1,求出m的范围即可判断,④令![]() ≤
≤![]() <﹣m,求出m的范围即可判断,⑤令
<﹣m,求出m的范围即可判断,⑤令![]() =﹣m,B,C重合,不合题意舍弃.⑥令
=﹣m,B,C重合,不合题意舍弃.⑥令![]() >﹣m,求出m的范围即可判断.
>﹣m,求出m的范围即可判断.
试题解析:(1)∵![]() =
=![]() ,
,![]() =
=![]() ,∴顶点坐标(
,∴顶点坐标(![]() ,
,![]() ).
).
(2)由 ,消去y得
,消去y得![]() ,∵抛物线与x轴有且仅有一个公共点,∴△=0,即(k﹣3)m=0,∵无论m取何值,方程总是成立,∴k﹣3=0,∴k=3;
,∵抛物线与x轴有且仅有一个公共点,∴△=0,即(k﹣3)m=0,∵无论m取何值,方程总是成立,∴k﹣3=0,∴k=3;
(3)PH=![]() =
=![]() ,∵1<PH≤6,∴当
,∵1<PH≤6,∴当![]() >0时,有1<
>0时,有1<![]() ≤6,又﹣1≤m≤4,∴
≤6,又﹣1≤m≤4,∴![]() <m≤
<m≤![]() ,当
,当![]() <0时,1<
<0时,1<![]() ≤6,又∵﹣1≤m≤4,∴﹣1≤m≤
≤6,又∵﹣1≤m≤4,∴﹣1≤m≤![]() ,∴﹣1≤m<
,∴﹣1≤m<![]() 或
或![]() <m≤
<m≤![]() ,∵A(﹣m﹣1,
,∵A(﹣m﹣1,![]() )在抛物线上,∴
)在抛物线上,∴![]() =﹣4m,∵C(﹣m,
=﹣4m,∵C(﹣m,![]() )在抛物线上,∴
)在抛物线上,∴![]() =﹣4m,∴
=﹣4m,∴![]() ;
;
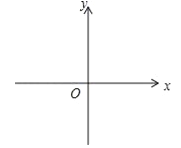
①令![]() <﹣m﹣1,则有m<
<﹣m﹣1,则有m<![]() ,结合﹣1≤m≤
,结合﹣1≤m≤![]() ,∴﹣1≤m<
,∴﹣1≤m<![]() ,此时,在对称轴的左侧y随x的增大而减小,如图1,∴
,此时,在对称轴的左侧y随x的增大而减小,如图1,∴![]() ,即当﹣1≤m<
,即当﹣1≤m<![]() 时,有
时,有![]() .
.
②令![]() =﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
=﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
③令![]() >﹣m﹣1,且
>﹣m﹣1,且![]() ≤
≤![]() 时,有
时,有![]() <m≤
<m≤![]() ,结合﹣1≤m<
,结合﹣1≤m<![]() ,∴
,∴![]() <m≤
<m≤![]() ,此时,在对称轴的左侧,y随x的增大而减小,如图2,∴
,此时,在对称轴的左侧,y随x的增大而减小,如图2,∴![]() ,即当
,即当![]() <m≤
<m≤![]() 时,有
时,有![]() ;
;
④令![]() ≤
≤![]() <﹣m,有
<﹣m,有![]() ≤m<0,结合﹣1≤m<
≤m<0,结合﹣1≤m<![]() ,∴
,∴![]() ≤m<
≤m<![]() ,此时,在对称轴的右侧y随x的增大而增大,如图3,∴
,此时,在对称轴的右侧y随x的增大而增大,如图3,∴![]() .
.
⑤令![]() =﹣m,B,C重合,不合题意舍弃.
=﹣m,B,C重合,不合题意舍弃.
⑥令![]() >﹣m,有m>0,结合
>﹣m,有m>0,结合![]() <m≤
<m≤![]() ,∴
,∴![]() <m≤
<m≤![]() ,此时,在对称轴的右侧,y随x的增大而增大,如图4,∴
,此时,在对称轴的右侧,y随x的增大而增大,如图4,∴![]() ,即当
,即当![]() <m≤
<m≤![]() 时,有
时,有![]() ;
;
综上所述,﹣1≤m<![]() 或
或![]() <m≤
<m≤![]() 时,有
时,有![]() ,
,![]() <m<
<m<![]() 时,有
时,有![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,已知AD=8,折叠纸片,使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
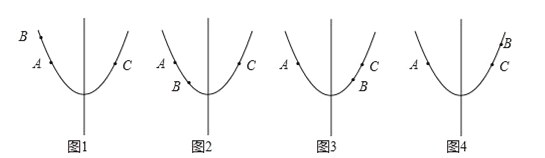
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
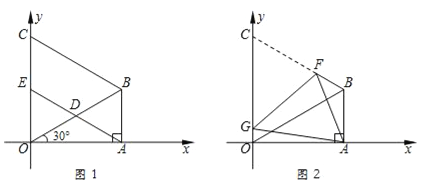
【题目】抛物线![]() 与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
与x轴交于A,B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,﹣3),B(4,0).
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,已知直线PA,PB与y轴分别交于E、F两点.当点P运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
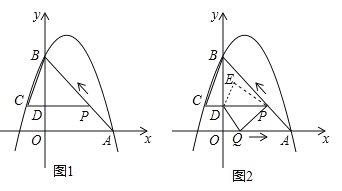
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(![]() ,
,![]() ),AB=1,AD=2.
),AB=1,AD=2.
(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数![]() (
(![]() )的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
)的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
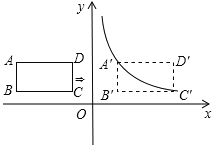
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com