
分析 (1)设每件衬衫应降价x元,则每件盈利(40-x)元,每天可以售出(20+2x),所以此时商场平均每天要盈利(40-x)(20+2x)元,根据商场平均每天要盈利=1200元,为等量关系列出方程求解即可.
(2)假设能达到,根据商场平均每天要盈利=1500元,为等量关系列出方程,看该方程是否有解,有解则说明能达到,否则不能.
解答 解:(1)设每件衬衫应降价x元,则每件盈利(40-x)元,每天可以售出(20+2x),
由题意,得(40-x)(20+2x)=1200,
即:(x-10)(x-20)=0,
解得x1=10,x2=20,
为了扩大销售量,增加盈利,尽快减少库存,所以x的值应为20,
所以,若商场平均每天要盈利12O0元,每件衬衫应降价20元;
(2)假设能达到,由题意,得(40-x)(20+2x)=1500,
整理,得x2-30x+350=0,
△=302-2×1×350=-500<0,
即:该方程无解,
所以,商场平均每天盈利不能达到1500元.
点评 本题主要考查一元二次方程的应用,关键在于理解清楚题意找出等量关系列出方程求解,另外还用到的知识点是“根的判别式”的应用.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
 如图,扇形OAB的圆心角∠AOB=120°,半径OA=6cm.
如图,扇形OAB的圆心角∠AOB=120°,半径OA=6cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
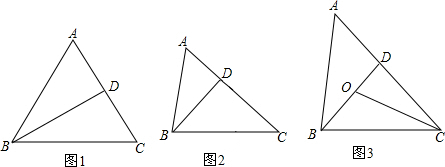
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
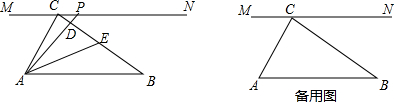
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com