
分析 (1)设大巴车的行驶速度为x千米/小时,则运货卡车的行驶速度为1.2x千米/小时,根据时间=路程÷速度结合二者所用时间之间的关系,即可得出关于x的分式方程,解之经检验后,即可得出结论;
(2)设若只由男生完成,男生平均每人应植树y棵,根据总人数=男生数+女生数结合人数=植树的棵数÷人均棵数,即可得出关于y的分式方程,解之并检验后,即可得出结论;
(3)由(2)的结论可求出该班男、女生人数之比,设A类小组有m个,根据男、女生人数之比,即可得出关于m的分式方程,解之并检验后,即可得出结论.
解答 解:(1)设大巴车的行驶速度为x千米/小时,则运货卡车的行驶速度为1.2x千米/小时,
根据题意得:$\frac{18}{x}$-$\frac{18}{1.2x}$=$\frac{2+2}{60}$,
解得:x=45,
经检验,x=45是原方程的解,且符合题意,
∴1.2x=54.
答:大巴车的行驶速度为45千米/小时,运货卡车的行驶速度为54千米/小时.
(2)设若只由男生完成,男生平均每人应植树y棵,
根据题意得:$\frac{1}{6}$=$\frac{1}{15}$+$\frac{1}{y}$,
解得:y=10,
经检验,y=10是原方程的解,且符合题意.
答:若只由男生完成,男生平均每人应植树10棵.
(3)男、女生人数之比为$\frac{1}{10}$:$\frac{1}{15}$=3:2,
设A类小组有m个,
根据题意得:$\frac{2m+n}{m+3n}$=$\frac{3}{2}$,
解得:m=7n,
经检验,m=7n是原方程的解,且符合题意.
答:A类小组有7n个.
点评 本题考查了分式方程的应用,解题的关键是:(1)根据时间=路程÷速度列出关于x的分式方程;(2)根据总人数=男生数+女生数列出关于y的分式方程;(3)根据男、女生人数之间的关系列出关于m的分式方程.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
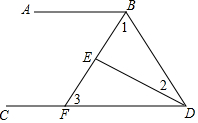 如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.
如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1+∠2=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com