
【题目】已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3). 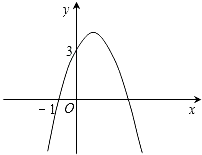
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
【答案】
(1)解:将点(﹣1,0),(0,3)代入y=﹣x2+bx+c中,得
![]() ,解得
,解得 ![]() .
.
∴y=﹣x2+2x+3
(2)解:令y=0,解方程﹣x2+2x+3=0,
得x1=﹣1,x2=3,抛物线开口向下,
∴当﹣1<x<3时,y>0
【解析】(1)把抛物线上的两点代入解析式,解方程组可求b、c的值;(2)令y=0,求抛物线与x轴的两交点坐标,观察图象,求y>0时,x的取值范围.
【考点精析】关于本题考查的二次函数的图象和抛物线与坐标轴的交点,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.


科目:初中数学 来源: 题型:
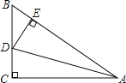
【题目】如图,在![]() ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB; ④BE+AC=AB.
ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB; ④BE+AC=AB.
一定成立的结论有____________(填序号) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方错误的是( )
A.x2+2x﹣99=0化为(x+1)2=100
B.![]()
C.x2+8x+9=0化为(x+4)2=25
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为4,边
的边长为4,边![]() 在
在![]() 轴上,边
轴上,边![]() 在
在![]() 轴上,点
轴上,点![]() 是
是![]() 轴上一点,坐标为
轴上一点,坐标为![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(1)点![]() 的坐标为;
的坐标为;
(2)判断![]() 的形状,并证明你的结论.
的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点P0的坐标为(![]() ,
,![]() ),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2017的坐标为( )
),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2017的坐标为( )

A. (![]() ,
,![]() ) B. (0,22018) C. (
) B. (0,22018) C. (![]() ,
,![]() ) D. (22018,0)
) D. (22018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,点P为BC边上一动点,连接AP,将线段AP绕P点顺时针旋转90°,点A恰好落在直线CD上点E处.
(1)如图1,点E在线段CD上,求证:AD+DE=2AB;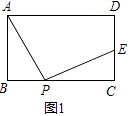
(2)如图2,点E在线段CD的延长线上,且点D为线段CE的中点,在线段BD上取点F,连接AF、PF,若AF=AB.求证:∠APF=∠ADB.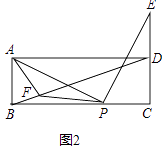
(3)如图3,点E在线段CD上,连接BD,若AB=2,BD∥PE,则DE= . (直接写出结果)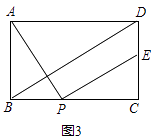
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com