
����Ŀ��ij�̳�����![]() ��
��![]() ������Ʒ���۳�2��
������Ʒ���۳�2��![]() ����Ʒ��3��
����Ʒ��3��![]() ����Ʒ��������Ϊ700Ԫ���۳�3��
����Ʒ��������Ϊ700Ԫ���۳�3��![]() ����Ʒ��5��
����Ʒ��5��![]() ����Ʒ��������Ϊ1100Ԫ��
����Ʒ��������Ϊ1100Ԫ��
��1����ÿ��![]() ����Ʒ��ÿ��
����Ʒ��ÿ��![]() ����Ʒ�۳�����������ֱ�Ϊ����Ԫ��
����Ʒ�۳�����������ֱ�Ϊ����Ԫ��
��2��������������![]() ��
��![]() ������Ʒ�ܿ����꣬�̳�������һ�ι���
������Ʒ�ܿ����꣬�̳�������һ�ι���![]() ��
��![]() ������Ʒ��34�����������34����Ʒȫ�����������������4000Ԫ����ô���̳������蹺�����ټ�
������Ʒ��34�����������34����Ʒȫ�����������������4000Ԫ����ô���̳������蹺�����ټ�![]() ����Ʒ��
����Ʒ��
���𰸡���1��ÿ��![]() ����Ʒ�۳������õ�����Ϊ200Ԫ��ÿ��
����Ʒ�۳������õ�����Ϊ200Ԫ��ÿ��![]() ����Ʒ�۳�����������Ϊ100Ԫ��
����Ʒ�۳�����������Ϊ100Ԫ��
��2���̳������蹺��6��![]() ����Ʒ
����Ʒ
��������
��1�����������г���Ԫһ�η�������⼴�ɣ�
��2�����������ҵ����ȹ�ϵ��������A+������B��4000���г�����ʽ���ɣ�
�⣺��1����ÿ��![]() ����Ʒ�۳�����������Ϊ
����Ʒ�۳�����������Ϊ![]() Ԫ��ÿ��
Ԫ��ÿ��![]() ����Ʒ�۳�����������Ϊ
����Ʒ�۳�����������Ϊ![]() Ԫ����������ã�
Ԫ����������ã�![]() ��
��
��ã�![]() ��
��
��ÿ��![]() ����Ʒ�۳������õ�����Ϊ200Ԫ��ÿ��
����Ʒ�۳������õ�����Ϊ200Ԫ��ÿ��![]() ����Ʒ�۳�����������Ϊ100Ԫ��
����Ʒ�۳�����������Ϊ100Ԫ��
��2���蹺��![]() ����Ʒ
����Ʒ![]() ������
������![]() ����Ʒ
����Ʒ![]() ����
����
��������ã�![]() ��
��
��ã�![]() ��
��
���̳������蹺��6��![]() ����Ʒ��
����Ʒ��


 �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д� �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��a��0����ͼ��A��1��0����B��3��0����C��0��6�����㣮
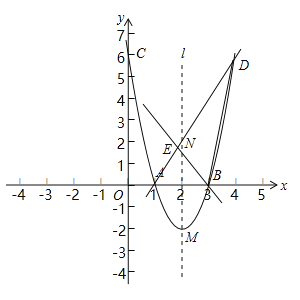
��1���������ߵĽ���ʽ��
��2�������ߵĶ���M��Գ���l�ϵĵ�N����x��Գƣ�ֱ��AN���������ڵ�D��ֱ��BE��AD�ڵ�E����ֱ��BE����ABD�������Ϊ1��2�����֣����E�����꣮
��3��PΪ�������ϵ�һ���㣬QΪ�Գ����϶��㣬���������Ƿ����һ��P��ʹA��D��P��QΪ������ı���Ϊƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
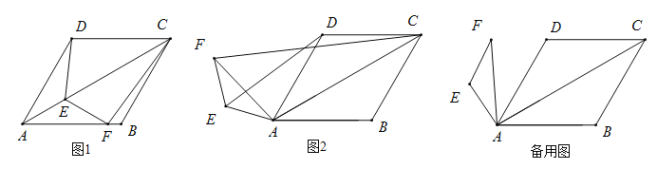
����Ŀ����ͼ1��������ABCD�У�![]() ����E��F�ֱ���AC��AB�ϵĵ㣬��
����E��F�ֱ���AC��AB�ϵĵ㣬��![]() �����룺
�����룺
����
��![]() ��ֵ��_______��
��ֵ��_______��
��ֱ��DE��ֱ��CF���ɵĽ��н�С�ĽǵĶ�����_______��
��2�����̽������ͼ2������![]() ��A��ʱ����ת������ת�Ĺ����У���1���н����Ƿ��������ͼ2������˵�����ɣ�
��A��ʱ����ת������ת�Ĺ����У���1���н����Ƿ��������ͼ2������˵�����ɣ�
��3����չ���죺
��![]() �Ƶ�A��ת�Ĺ����У���
�Ƶ�A��ת�Ĺ����У���![]() ���㹲��ʱ����ֱ��д��CF�ij���
���㹲��ʱ����ֱ��д��CF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������飬���ľ����飬����״������Ⱦ�ķ��������ڼ䣬ij��ѧ�������μ��װ��Ļ���ð�50��ѧ���ľ��ͳ��������±���
���/Ԫ | 5 | 10 | 20 | 50 | 100 |
���� | 6 | 17 | 14 | 8 | 5 |
�����Ǿ�������������λ���ֱ���( )
A.100��10B.10��20C.17��10D.17��20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
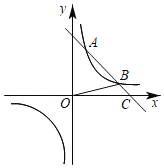
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y����x+b��ͼ���뷴��������![]() ��k��0����ͼ���ཻ��A��B���㣬��x���ཻ�ڵ�C(4��0)���ҵ�B(3��n)������OB��
��k��0����ͼ���ཻ��A��B���㣬��x���ཻ�ڵ�C(4��0)���ҵ�B(3��n)������OB��
��1����һ�κ����ͷ����������ı���ʽ��
��2�����BOC�������
��3����ֱ��AB����ƽ�ƣ���ƽ�ƺ��ֱ���뷴����������ͼ��ֻ��һ�����㣬��˵��ֱ��AB����ƽ���˼�����λ���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() Ϊһ������ֽƬ��
Ϊһ������ֽƬ��![]() ��
��![]() ������
������![]() ��
��![]() �������
�������![]() �����˶���
�����˶���![]() ���ֹͣ��
���ֹͣ��![]() ��ֱ��
��ֱ��![]() Ϊ�ᷭ�ۣ���
Ϊ�ᷭ�ۣ���![]() ���ڵ�
���ڵ�![]() ��λ�ã���
��λ�ã���![]() ��
��![]() ��ԭֽƬ�ص����ֵ����Ϊ
��ԭֽƬ�ص����ֵ����Ϊ![]() ��
��
��1����![]() Ϊ��ֵʱ��ֱ��
Ϊ��ֵʱ��ֱ��![]() ����
����![]() ��
��
��2����![]() Ϊ��ֵʱ��ֱ��
Ϊ��ֵʱ��ֱ��![]() ��
��![]() ���е�
���е�![]() ��
��
��3�����![]() ��
��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ������![]() ������
������![]() ��̺��
��̺��![]() ��������
��������![]() �������������������Ϊ�˽�ѧ�����������������ϲ���������ȫУ��Χ�������ȡ������ѧ���������ʾ����飨ÿ���������ͬѧ����ѡ�����ֻ����
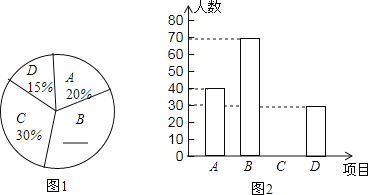
�������������������Ϊ�˽�ѧ�����������������ϲ���������ȫУ��Χ�������ȡ������ѧ���������ʾ����飨ÿ���������ͬѧ����ѡ�����ֻ����![]() ���������ѡ��һ�֣��������ݽ������������Ƴ���������ͳ��ͼ��δ��������
���������ѡ��һ�֣��������ݽ������������Ƴ���������ͳ��ͼ��δ��������
��1����ε����У�һ�������� ��ѧ����
��2���벹ȫ����ͳ��ͼ��
��3������![]() ����ϲ��̺���˶���ѧ����
����ϲ��̺���˶���ѧ����![]() ����ϲ�������˶���ѧ���������μ�һ��������������ѡ��
����ϲ�������˶���ѧ���������μ�һ��������������ѡ��![]() �˵����鳤����������������
�˵����鳤����������������![]() �˾�����ϲ�������˶���ѧ���ĸ���
�˾�����ϲ�������˶���ѧ���ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
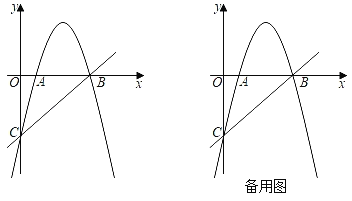
����Ŀ����ͼ��������y��ax2+6x+c��x����A��B���㣬��y���ڵ�C��ֱ��y��x��5������B��C��
��1���������ߵĽ���ʽ��
��2������NΪ�������϶��㣬����NBA����OACʱ�����N�����꣬
��3������A��ֱ�߽�ֱ��BC�ڵ�M����AM��BCʱ������������һ����P�������B��C�غϣ�����ֱ��AM��ƽ���߽�ֱ��BC�ڵ�Q�����Ե�A��M��Q��PΪ������ı�����ƽ���ı��Σ����P�ĺ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
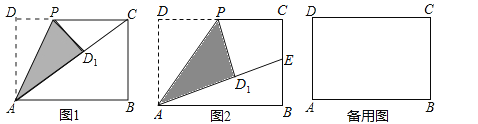
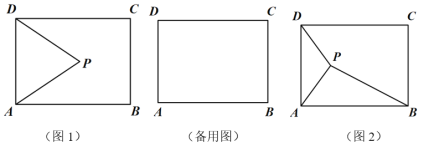
����Ŀ�����Ķ����⣩���P�ھ���ABCD�ڲ�������P�����ε�һ���ߵ������˵�������ʱ���Ƶ�PΪ�ñߵ�����г���������磺��ͼ1������ABCD�У���PA��PD�����PΪ��AD������г������
���������ã���֪����P�ھ���ABCD�ڲ�����AB=10��BC=6��
��1����P�DZ�AD�������������P ��BC���������������������������������
��2����P�DZ�BC������г����������PA��PB������PAB��ֱ��������ʱ����PA��ֵ��
��3����ͼ2����P�DZ�AD������г����������PA��PB��PD����tan��PAB�� tan��PBA����Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com