
 如图,某地有一座圆弧形的拱桥,圆弧所在圆的圆心为O,半径为OC,桥下水面宽AB为7.2m,拱顶C高出2.4m(CD=2.4m),现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船DFNM要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
如图,某地有一座圆弧形的拱桥,圆弧所在圆的圆心为O,半径为OC,桥下水面宽AB为7.2m,拱顶C高出2.4m(CD=2.4m),现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船DFNM要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由. 解:如图,连接ON,OB.
解:如图,连接ON,OB.| 1 |
| 2 |
| 2.96 |
| 2.96 |


科目:初中数学 来源: 题型:
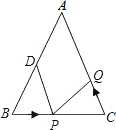 如图,在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以1cm/s的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.
如图,在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以1cm/s的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.查看答案和解析>>
科目:初中数学 来源: 题型:
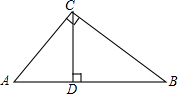 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h.求证:
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h.求证:| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com