
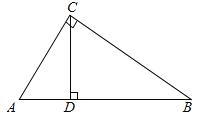
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬”ĻC£½90”ć£¬AC£½3£¬BC£½4£¬CDŹĒŠ±±ßABÉĻµÄøߣ¬µćEŌŚŠ±±ßABÉĻ£¬¹żµćE×÷Ö±ĻßÓė”÷ABCµÄÖ±½Ē±ßĻą½»ÓŚµćF£¬ÉčAE£½x£¬”÷AEFµÄĆ껿ĪŖy£®
£Ø1£©CD= £¬AD= £»
£Ø2£©ČōEF”ĶAB£¬µ±µćEŌŚĻ߶ĪABÉĻŅĘ¶ÆŹ±£»
¢ŁĒóyÓėxµÄŗÆŹż¹ŲĻµŹ½£»£ØŠ“³ö×Ō±äĮæxµÄȔֵ·¶Ī§£©
¢Śµ±xČ”ŗĪÖµŹ±£¬yÓŠ×ī“óÖµ£æ²¢ĒóĘä×ī“óÖµ
£Ø3£©ČōFŌŚÖ±½Ē±ßACÉĻ£ØµćFÓėA”¢CĮ½µć¾ł²»ÖŲŗĻ£©£¬µćEŌŚŠ±±ßABÉĻŅĘ¶Æ£¬ŹŌĪŹ£ŗŹĒ·ń“ęŌŚÖ±ĻßEF½«”÷ABCµÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö£æČō“ęŌŚÖ±ĻßEF£¬Ēó³öxµÄÖµ£»Čō²»“ęŌŚÖ±ĻßEF£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©![]() £¬
£¬![]() £»£Ø2£©¢Ł
£»£Ø2£©¢Ł £»¢Śµ±x£½
£»¢Śµ±x£½![]() £¼5Ź±£¬
£¼5Ź±£¬![]() ×ī“ó£½
×ī“ó£½![]() £»£Ø3£©“ęŌŚ£¬
£»£Ø3£©“ęŌŚ£¬![]()
”¾½āĪö”æ
£Ø1£©ĻČøł¾Ż¹“¹É¶ØĄķĒó³öABµÄ³¤£¬ŌŁøł¾ŻRt”÷ADC”×Rt”÷ACB£¬ĄūÓĆĘäĻąĖĘ±Č¼“æÉĒó³öADµÄ³¤£»
£Ø2£©¢Ł·Ö±šøł¾ŻxµÄȔֵ·¶Ī§¼°Čż½ĒŠĪµÄĆ껿¹«Ź½·ÖĄąæɵĆx”¢yµÄŗÆŹż¹ŲĻµŹ½£»
¢Śøł¾Ż¢ŁÖŠĖłĒóµÄŗÆŹż¹ŲĻµŹ½Ēó³öĘä×īÖµ¼“æÉ£®
£Ø3£©ĻČĒóµĆ”÷ABCµÄĆ껿µÄ![]() £¬½ų¶ųµĆµ½”÷AEFµĆµ½Ć껿µÄŗÆŹż¹ŲĻµŹ½£¬ČĆĖüµČÓŚ3£¬ĮŠŹ½¼“æÉĒó½ā£®
£¬½ų¶ųµĆµ½”÷AEFµĆµ½Ć껿µÄŗÆŹż¹ŲĻµŹ½£¬ČĆĖüµČÓŚ3£¬ĮŠŹ½¼“æÉĒó½ā£®
½ā£ŗ£Ø1£©”ß”÷ABCÖŠ£¬”ĻC£½90”ć£¬AC£½3£¬BC£½4£¬
”ąAB£½![]() £½5£¬
£½5£¬
”ßCD”ĶAB£¬
”ą”ĻCDA£½”ĻACB£½90”ć£¬
ÓÖ”ĻCAD£½”ĻCAD£¬
”ąRt”÷ADC”×Rt”÷ACB£¬
”ą![]() £¬¼“
£¬¼“![]() £¬
£¬
”ąCD£½![]() £¬AD£½
£¬AD£½![]() £®
£®
£Ø2£©¢ŁÓÉÓŚEµÄĪ»ÖĆ²»ÄÜČ·¶Ø£¬¹ŹÓ¦·ÖĮ½ÖÖĒéæöĢÖĀŪ£ŗ
ČēĶ¼A£ŗµ±0£¼x”ÜAD£¬¼“0£¼x”Ü![]() Ź±£¬
Ź±£¬
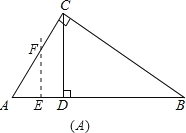
”ßEF”ĶAB£¬
”ąRt”÷AEF”×Rt”÷ACB£¬¼“![]() £¬
£¬
”ßAC£½3£¬BC£½4£¬AE£½x£¬
”ą![]() £¬EF£½
£¬EF£½![]() x£¬
x£¬
S”÷AEF£½y£½![]() £®
£®
ČēĶ¼B£ŗµ±AD£¼x”ÜAB£¬¼“![]() £¼x”Ü5Ź±£¬
£¼x”Ü5Ź±£¬
”ßEF”ĶAB£¬
”ąRt”÷BEF”×Rt”÷BCA£¬
”ą![]() £¬
£¬
”ßAE£½x£¬”÷AEFµÄĆ껿ĪŖy£¬![]() £¬
£¬
”ąEF£½![]() £¬
£¬
![]() £®
£®
¢Śµ±ČēĶ¼A£ŗµ±0£¼x”ÜAD£¬¼“0£¼x”Ü![]() Ź±£¬
Ź±£¬
![]() £¬
£¬
µ±x£½AD£¬¼“x£½![]() Ź±£¬y×ī“ó£½
Ź±£¬y×ī“ó£½![]() £®
£®
ČēĶ¼B£ŗµ±AD£¼x”ÜBD£¬¼“![]() £¼x”Ü5Ź±£¬
£¼x”Ü5Ź±£¬
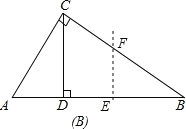
![]() £¬y×ī“ó£½
£¬y×ī“ó£½![]() £¬“ĖŹ±x£½2.5£¼5£¬¹Ź³ÉĮ¢£®
£¬“ĖŹ±x£½2.5£¼5£¬¹Ź³ÉĮ¢£®
¹Źy×ī“ó£½![]() £®
£®
£Ø3£©“ęŌŚ£®
¼ŁÉč“ęŌŚ£¬µ±0£¼x”Ü5Ź±£¬
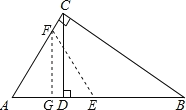
”ß”÷ABCµÄÖܳ¤ĪŖ3+4+5£½12£¬
”ąAE+AF£½6£¬
”ąAF£½6©x£¬”ą0£¼6©x£¼3£¬
”ą3£¼x£¼6£¬
”ą3£¼x”Ü5£¬
×÷FG”ĶABÓŚµćG£¬
ÓÉ”÷AFG”×”÷ACD£¬
”ą![]() £¬
£¬
”ą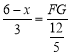 £¬
£¬
¼“FG£½![]() £Ø6©x£©£¬
£Ø6©x£©£¬
”ąS”÷AEF£½![]() £¬
£¬
”ą3£½![]() £¬
£¬
½āµĆ£ŗx1£½![]() £¬x2£½
£¬x2£½![]() £¬
£¬
”ß3£¼x”Ü5£¬
”ąx1£½![]() £Ø·ūŗĻĢāŅā£©£¬x2£½
£Ø·ūŗĻĢāŅā£©£¬x2£½![]() £Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬
£Ø²»ŗĻĢāŅā£¬ÉįČ„£©£¬
¹Ź“ęŌŚx£¬Ö±ĻßEF½«”÷ABCµÄÖܳ¤ŗĶĆ껿Ķ¬Ź±Ę½·Ö£¬“ĖŹ±x£½![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijµēŹÓĢØĪŖĮĖ½ā±¾µŲĒųµēŹÓ½ŚÄæµÄŹÕŹÓĒéæö£¬¶Ō²æ·ÖŹŠĆńæŖÕ¹ĮĖ”°Äć×īĻ²°®µÄµēŹÓ½ŚÄæ”±µÄĪŹ¾ķµ÷²é£ØĆæČĖÖ»ĢīŠ“Ņ»Ļī£©£¬øł¾ŻŹÕ¼ÆµÄŹż¾Ż»ęÖĘĮĖĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£ØČēĶ¼ĖłŹ¾£©£¬øł¾ŻŅŖĒó»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©±¾“ĪĪŹ¾ķµ÷²é¹²µ÷²éĮĖ________Ćū¹ŪÖŚ£»Ķ¼¢ŚÖŠ×īĻ²°®”°ŠĀĪŽŚÄæ”±µÄČĖŹżÕ¼µ÷²é×ÜČĖŹżµÄ°Ł·Ö±ČĪŖ________£»
£Ø2£©²¹Č«Ķ¼¢ŁÖŠµÄĢõŠĪĶ³¼ĘĶ¼£»
£Ø3£©ĻÖÓŠ×īĻ²°®”°ŠĀĪŽŚÄæ”±£Ø¼ĒĪŖ![]() £©£¬”°ĢåÓż½ŚÄæ”±£Ø¼ĒĪŖ
£©£¬”°ĢåÓż½ŚÄæ”±£Ø¼ĒĪŖ![]() £©£¬”°×ŪŅÕ½ŚÄæ”±£Ø¼ĒĪŖ
£©£¬”°×ŪŅÕ½ŚÄæ”±£Ø¼ĒĪŖ![]() £©£¬”°æĘĘÕ½ŚÄæ”±£Ø¼ĒĪŖ
£©£¬”°æĘĘÕ½ŚÄæ”±£Ø¼ĒĪŖ![]() £©µÄ¹ŪÖŚø÷Ņ»Ćū£¬µēŹÓĢØŅŖ“ÓĖÄČĖÖŠĖ껜³éČ”Į½ČĖ²Ī¼ÓĮŖŅź»ī¶Æ£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·Ø£¬Ēó³öĒ”ŗĆ³éµ½×īĻ²°®”°
£©µÄ¹ŪÖŚø÷Ņ»Ćū£¬µēŹÓĢØŅŖ“ÓĖÄČĖÖŠĖ껜³éČ”Į½ČĖ²Ī¼ÓĮŖŅź»ī¶Æ£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·Ø£¬Ēó³öĒ”ŗĆ³éµ½×īĻ²°®”°![]() ”±ŗĶ”°
”±ŗĶ”°![]() ”±Į½Ī»¹ŪÖŚµÄøÅĀŹ.
”±Į½Ī»¹ŪÖŚµÄøÅĀŹ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
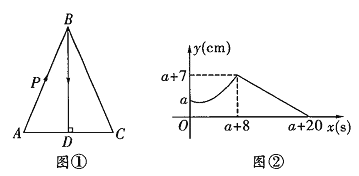
”¾ĢāÄæ”æ ʶĄ§»§ĄĻĶõŌŚ¾«×¼·öʶ¹¤×÷¶ÓµÄ°ļ·öĻĀ£¬ŌŚŅ»Ę¬ĶĮµŲÉĻÖÖÖ²ĮĖÓÅÖŹĖ®¹ūĄ¶Ż®£¬¾ŗĖĖć£¬ÖÖÖ²³É±¾ĪŖ18ŌŖ/Ē§æĖ£®½ńÄźÕżŹ½ÉĻŹŠĻśŹŪ£¬Ķعż30ĢģµÄŹŌĻś·¢ĻÖ£ŗµŚ1ĢģĀō³ö20Ē§æĖ£»ŅŌŗóĆæĢģ±ČĒ°Ņ»Ģģ¶ąĀō4Ē§æĖ£¬ĻśŹŪ¼Ūøń![]() ŌŖ/Ē§æĖ£©ÓėŹ±¼äx£ØĢģ£©Ö®¼äĀś×ćČēĻĀ±ķ£ŗ
ŌŖ/Ē§æĖ£©ÓėŹ±¼äx£ØĢģ£©Ö®¼äĀś×ćČēĻĀ±ķ£ŗ
Ź±¼ä | (1”Üx£¼20£© | (20”Üx”Ü30£© |
ĻśŹŪ¼Ūøńy£ØŌŖ/Ē§æĖ£© | -0.5x+38 | 25 |
£ØĘäÖŠ£¬x£¬y¾łĪŖÕūŹż£©
£Ø1£©ŹŌĻśÖŠĻśŹŪĮæP£ØĒ§æĖ£©ÓėŹ±¼ä![]() £ØĢģ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ £®
£ØĢģ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ £®
£Ø2£©ĒóĻśŹŪĄ¶Ż®µŚ¼øĢģŹ±£¬µ±ĢģµÄĄūČów×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁŌŖ£æ
£Ø3£©ĒóŹŌĻśµÄ30ĢģÖŠ£¬µ±ĢģĄūČów²»µĶÓŚ870ŌŖµÄĢģŹż¹²ÓŠ¼øĢģ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
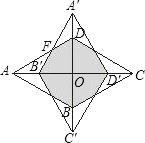
”¾ĢāÄæ”æČēĶ¼,ŌŚĮāŠĪABCDÖŠ,”ĻBAD=60”ć,¶Ō½ĒĻßAC”¢BDĻą½»ÓŚµćO½«ĘäČĘ×ŵćOĖ³Ź±ÕėŠż×Ŗ90”ćµĆµ½ĮāŠĪA”®B”ÆC”®D”Æ.ČōAB=1,ŌņŠż×ŖĒ°ŗóĮ½ĮāŠĪÖŲµž²æ·ÖĶ¼ŠĪµÄÖܳ¤ĪŖ__________
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅĻŲŹµŹ©ŠĀæĪ³ĢøÄøļŗó£¬Ń§Ļ°µÄ×ŌÖ÷×ÖĻ°”¢ŗĻ×÷½»Į÷ÄÜĮ¦ÓŠŗÜ“óĢįøߣ¬ÕÅĄĻŹ¦ĪŖĮĖĮĖ½āĖł½Ģ°ą¼¶Ń§Éś×ŌÖ÷ѧĻ°”¢ŗĻ×÷½»Į÷µÄ¾ßĢåĒéæö£¬¶Ō±¾°ą²æ·Öѧɜ½ųŠŠĮĖĪŖĘŚ°ėøöŌĀµÄøś×Łµ÷Ė£¬²¢½«µ÷Ė½į¹ū·Ö³ÉĖÄĄą£¬A£ŗĢŲ±šŗĆ£»B£ŗŗĆ£»C£ŗŅ»°ć£»D£ŗ½Ļ²ī£»²¢½«µ÷Ė½į¹ū»ęÖĘ³ÉŅŌĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬ĒėÄćøł¾ŻĶ³¼ĘĶ¼ĻĀĮŠĪŹĢā£ŗ

£Ø1£©±¾“Īµ÷²éÖŠ£¬ÕÅĄĻŹ¦Ņ»¹²µ÷ĖĮĖ””””ĆūĶ¬Ń§£¬ĘäÖŠCĄąÅ®ÉśÓŠ””””Ćū£¬DĄąÄŠÉśÓŠ””””Ćū£»
£Ø2£©½«ÉĻĆęµÄĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©ĪŖĮĖ¹²Ķ¬½ų²½£¬ÕÅĄĻŹ¦Ļė“Ó±»µ÷ĖµÄAĄąŗĶDĄąŃ§ÉśÖŠ·Ö±šŃ”Č”Ņ»Ī»Ķ¬Ń§±ÅŠŠ”°Ņ»°ļŅ»”±»„֜ѧĻ°£¬ĒėÓĆĮŠ±ķ·Ø»ņ»Ź÷ŠĪĶ¼µÄ·½·ØĒó³öĖłŃ”Į½Ī»Ķ¬Ń§Ē”ŗĆŹĒŅ»Ī»ÄŠĶ¬Ń§ŗĶŅ»Ī»Å®Ķ¬Ń§µÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¾ŲŠĪ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() £¬£Ø
£¬£Ø![]() £©£¬ŅŌ
£©£¬ŅŌ![]() ĪŖŠż×ŖÖŠŠÄĖ³Ź±ÕėŠż×Ŗ¾ŲŠĪ
ĪŖŠż×ŖÖŠŠÄĖ³Ź±ÕėŠż×Ŗ¾ŲŠĪ![]() £¬µĆµ½¾ŲŠĪ
£¬µĆµ½¾ŲŠĪ![]() £®
£®
£Ø1£©ČēĶ¼1£¬µ±µć![]() ĀäŌŚ±ß
ĀäŌŚ±ß![]() ÉĻŹ±£¬Ēó
ÉĻŹ±£¬Ēó![]() µÄ³¤£»
µÄ³¤£»
£Ø2£©ČēĶ¼2£¬µ±![]() Ź±£¬¾ŲŠĪ
Ź±£¬¾ŲŠĪ![]() µÄ¶Ō½ĒĻß
µÄ¶Ō½ĒĻß![]() ½»¾ŲŠĪ
½»¾ŲŠĪ![]() µÄ±ß
µÄ±ß![]() ÓŚµć
ÓŚµć![]() £¬Į¬½į
£¬Į¬½į![]() £¬Čō
£¬Čō![]() ŹĒµČŃüČż½ĒŠĪ£¬ĒóÖ±Ļß
ŹĒµČŃüČż½ĒŠĪ£¬ĒóÖ±Ļß![]() µÄ½āĪöŹ½£®
µÄ½āĪöŹ½£®
£Ø3£©ČēĶ¼3£¬µ±![]() Ź±£¬¾ŲŠĪ
Ź±£¬¾ŲŠĪ![]() µÄ¶Ō³ĘÖŠŠÄĪŖµć
µÄ¶Ō³ĘÖŠŠÄĪŖµć![]() £®
£®![]() µÄĆ껿ĪŖ
µÄĆ껿ĪŖ![]() £¬Ēó
£¬Ēó![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪÖ½Ę¬![]() µÄ±ß³¤ĪŖ
µÄ±ß³¤ĪŖ![]() £¬·ÕŪ
£¬·ÕŪ![]() £¬Ź¹Į½øöÖ±½Ē¶„µćÖŲŗĻÓŚ¶Ō½ĒĻß
£¬Ź¹Į½øöÖ±½Ē¶„µćÖŲŗĻÓŚ¶Ō½ĒĻß![]() ÉĻŅ»µć
ÉĻŅ»µć![]() ·Ö±šŹĒÕŪŗŪ£¬Éč
·Ö±šŹĒÕŪŗŪ£¬Éč![]() £¬øų³öĻĀĮŠÅŠ¶Ļ£ŗ
£¬øų³öĻĀĮŠÅŠ¶Ļ£ŗ
¢Łµ±![]() Ź±£¬µć
Ź±£¬µć![]() ŹĒÕż·½ŠĪ
ŹĒÕż·½ŠĪ![]() µÄÖŠŠÄ£»
µÄÖŠŠÄ£»
¢Śµ±![]() Ź±£¬
Ź±£¬![]() £»
£»
¢Ūµ±![]() Ź±£¬Įł±ßŠĪ
Ź±£¬Įł±ßŠĪ![]() Ć껿µÄ×ī“óÖµŹĒ
Ć껿µÄ×ī“óÖµŹĒ![]()
¢Üµ±![]() Ź±£¬Įł±ßŠĪ
Ź±£¬Įł±ßŠĪ![]() Öܳ¤µÄÖµ²»±ä£®
Öܳ¤µÄÖµ²»±ä£®
ĘäÖŠ“ķĪóµÄŹĒ£Ø £©

A.¢Ś¢ŪB.¢Ū¢ÜC.¢Ł¢ÜD.¢Ł¢Ś
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼![]() £¬ŌŚ
£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() ŹĒ
ŹĒ![]() µÄøßĻߣ¬µć
µÄøßĻߣ¬µć![]() “Ó
“Ó![]() µÄ
µÄ![]() µć³ö·¢£¬ŃŲ
µć³ö·¢£¬ŃŲ![]() µÄ·½ĻņŅŌ
µÄ·½ĻņŅŌ![]() µÄĖŁ¶ČŌČĖŁŌĖ¶Æµ½µć
µÄĖŁ¶ČŌČĖŁŌĖ¶Æµ½µć![]() Ķ¼
Ķ¼![]() ŹĒµć
ŹĒµć![]() ŌĖ¶ÆŹ±£¬
ŌĖ¶ÆŹ±£¬![]() µÄ³¤
µÄ³¤![]() Ėꏱ¼ä
Ėꏱ¼ä![]() ±ä»ÆµÄ¹ŲĻµĶ¼Ļó£¬Ōņ
±ä»ÆµÄ¹ŲĻµĶ¼Ļó£¬Ōņ![]() µÄĆ껿ĪŖ£Ø £©
µÄĆ껿ĪŖ£Ø £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£¬Rt”÷ABCÖŠ£¬”ĻACB£½90”ć£¬AC£½5£¬BC£½12£¬µćDŌŚ±ßABÉĻ£¬ŅŌADĪŖÖ±¾¶µÄ”ŃO£¬Óė±ßBCÓŠ¹«¹²µćE£¬ŌņADµÄ×īŠ”ÖµŹĒ_____£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com