
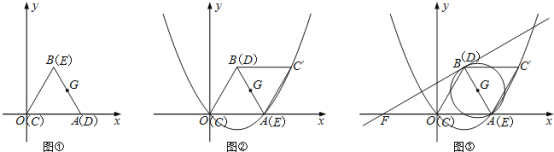
【题目】如图①②,在平面直角坐标系中,边长为2的等边![]() 恰好与坐标系中的
恰好与坐标系中的![]() 重合,现将
重合,现将![]() 绕边
绕边![]() 的中点
的中点![]() 点也是
点也是![]() 的中点),按顺时针方向旋转
的中点),按顺时针方向旋转![]() 到△
到△![]() 的位置.
的位置.
(1)求![]() 点的坐标;
点的坐标;
(2)求经过三点![]() 、
、![]() 、
、![]() 的抛物线的解析式;
的抛物线的解析式;
(3)如图③,![]() 是以
是以![]() 为直径的圆,过
为直径的圆,过![]() 点作
点作![]() 的切线与
的切线与![]() 轴相交于点
轴相交于点![]() ,求切线
,求切线![]() 的解析式;
的解析式;
(4)抛物线上是否存在一点![]() ,使得
,使得![]() .若存在,请求出点
.若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4) .
.
【解析】
(1)利用中心对称图形的性质和等边三角形的性质,可以求出.
(2)运用待定系数法,代入二次函数解析式,即可求出.
(3)借助切线的性质定理,直角三角形的性质,求出F,B的坐标即可求出解析式.
(4)当M在x轴上方或下方,分两种情况讨论.
解:(1)将等边![]() 绕边
绕边![]() 的中点
的中点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 到△
到△![]() ,
,
则有,四边形![]() 是菱形,所以
是菱形,所以![]() 的横坐标为3,
的横坐标为3,
根据等边![]() 的边长是2,
的边长是2,
利用等边三角形的性质可得![]() ;
;
(2)![]() 抛物线过原点
抛物线过原点![]() ,设抛物线解析式为
,设抛物线解析式为![]() ,
,
把![]() ,
,![]() 代入,得
代入,得 ,
,
解得![]() ,
,![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
(3)![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() ,
,![]() 代入,得
代入,得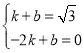 ,
,
解得![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ;
;
(4)①当![]() 在
在![]() 轴上方时,存在
轴上方时,存在![]() ,
,
![]() ,
,
得![]() ,解得
,解得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,![]() ;
;
②当![]() 在
在![]() 轴下方时,不存在,设点
轴下方时,不存在,设点![]() ,
,
![]() ,
,
得![]() ,
,![]() 无解,
无解,
综上所述,存在点的坐标为![]() ,
,![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,E是矩形ABCD的边BC上一点,EF⊥AE,分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=4,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
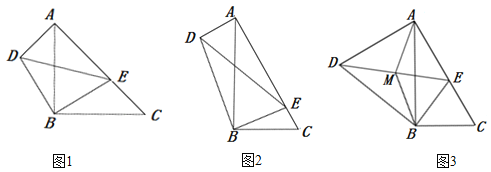
【题目】(1)问题发现
如图1,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=45°,点E是线段AC上一动点,连接DE.
填空:①则![]() 的值为______;②∠EAD的度数为_______.
的值为______;②∠EAD的度数为_______.
(2)类比探究
如图2,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=60°,点E是线段AC上一动点,连接DE.请求出![]() 的值及∠EAD的度数;
的值及∠EAD的度数;
(3)拓展延伸
如图3,在(2)的条件下,取线段DE的中点M,连接AM、BM,若BC=4,则当△ABM是直角三角形时,求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
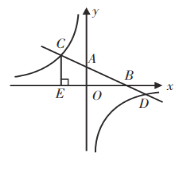
【题目】已知:如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() ,
,![]() 轴交于点
轴交于点![]() ,
,![]() ,与反比例函数的图象分别交于点
,与反比例函数的图象分别交于点![]() ,
,![]() ,
, ![]() 轴于点
轴于点![]() ,
, ![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)求反比例函数的解析式;
(3)连接![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠C=90°,请用直尺和圆规作一条直线,把△ABC分割成两个等腰三角形(不写作法,但须保留作图痕迹).
(2)已知内角度数的两个三角形如图2,图3所示.请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请写出分割成的两个等腰三角形顶角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,民勤电视台为此进行过专访报到.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:![]() .非常赞同;
.非常赞同;![]() .赞同但要有时间限制;
.赞同但要有时间限制;![]() .无所谓;
.无所谓;![]() .不赞同.并将调查结果绘制了图①和图②两幅不完整的统计图.请你根据图中提供的信息解答下列问题:
.不赞同.并将调查结果绘制了图①和图②两幅不完整的统计图.请你根据图中提供的信息解答下列问题:

(1)求本次被抽查的居民有多少人?
(2)将图①和图②补充完整.
(3)求图②中“![]() ”层次所在扇形的圆心角度数.
”层次所在扇形的圆心角度数.
(4)估计该小区5000名居民中对“广场舞”的看法表示赞同(包括![]() 层次和
层次和![]() 层次)的大约有多少人.
层次)的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
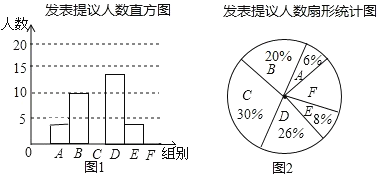
【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
(1)求得样本容量为 ,并补全直方图;
(2)已知A组发表提议的代表中恰有1位女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在近期“抗疫”期间,某药店销售A、B两种型号的口罩,已知销售800只A型和450只B型的利润为210元,销售400只A型和600只B型的利润为180元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不超过A型口罩的3倍,设购进A型口罩x只,这2000只口罩的销售总利润为y元.
①求y关于x的函数关系式;
②该药店购进A型、B型口罩各多少只,才能使销售总利润最大?
(3)在销售时,该药店开始时将B型口罩提价100%,当收回成本后,为了让利给消费者,决定把B型口罩的售价调整为进价的15%,求B型口罩降价的幅度.
查看答案和解析>>
科目:初中数学 来源: 题型:
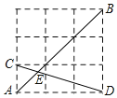
【题目】如图,在由边长为1的小正方形组成的网格中.点 A,B,C,D 都在这些小正方形的格点上,AB、CD 相交于点E,则sin∠AEC的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com