
 如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,$\sqrt{3}$≈1.7).
如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,$\sqrt{3}$≈1.7). 分析 作BF⊥AE于F,则FE=BD=6.4米,DE=BF,设BF=x米,则AF=AF=$\sqrt{3}$x米,在Rt△ABF中,由勾股定理得出方程,解方程求出DE=BF=8米,AF≈13.6米,得出AE的长度,在Rt△ACE中,由三角函数求出CE,即可得出结果.
解答 解:作BF⊥AE于F,如图所示: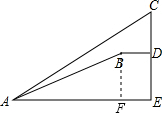 则FE=BD=6.4米,DE=BF,
则FE=BD=6.4米,DE=BF,
∵斜坡AB的坡角为30°,
∴AF=$\sqrt{3}$BF,
设BF=x米,则AF=$\sqrt{3}$x米,
在Rt△ABF中,由勾股定理得:x2+($\sqrt{3}$x)2=162,
解得:x=8,
∴DE=BF=8米,AF≈13.6米,
∴AE=AF+FE=20米,
在Rt△ACE中,CE=AE•tan36°≈20×0.73=14.6米,
∴CD=CE-DE=14.6-8=6.6米.
故大树CD的高度约为6.6米.
点评 本题考查了解直角三角形的应用、勾股定理、三角函数;由勾股定理得出方程是解决问题的关键.


科目:初中数学 来源: 题型:解答题
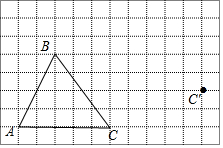 如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.(利用网格点和三角板画图)
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.(利用网格点和三角板画图)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
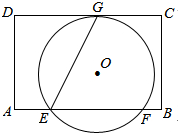 如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=$\frac{1}{4}$AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=$\sqrt{5}$:2.当⊙O与边BC所在的直线与相切时,AB的长是12.
如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=$\frac{1}{4}$AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=$\sqrt{5}$:2.当⊙O与边BC所在的直线与相切时,AB的长是12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
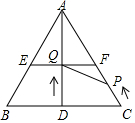 如图.在△ABC中.AB=AC=5cm,BC=6cm,AD是BC边上的高.点P由C出发沿CA方向匀速运动.速度为1cm/s.同时,直线EF由BC出发沿DA方向匀速运动.速度为1cm/s,EF∥BC,并且EF分别交AB、AD、AC于点E,Q,F,连接PQ.若设运动时间为t(s)(0<t<4),解答下列问题:
如图.在△ABC中.AB=AC=5cm,BC=6cm,AD是BC边上的高.点P由C出发沿CA方向匀速运动.速度为1cm/s.同时,直线EF由BC出发沿DA方向匀速运动.速度为1cm/s,EF∥BC,并且EF分别交AB、AD、AC于点E,Q,F,连接PQ.若设运动时间为t(s)(0<t<4),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
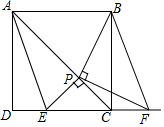 如图,在正方形ABCD中.点P是对角线AC上一个动点(不与点A,C重合),连接PB,过点P作PF⊥PB,交直线DC于点F.作PE⊥AC交直线DC于点E.连按AE,BF.
如图,在正方形ABCD中.点P是对角线AC上一个动点(不与点A,C重合),连接PB,过点P作PF⊥PB,交直线DC于点F.作PE⊥AC交直线DC于点E.连按AE,BF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
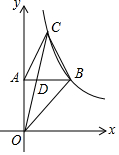 如图,B、C两点都在反比例函数y=$\frac{k}{x}$(x>0)上,点A在y轴上,AB∥x轴,当△ABC是等边三角形时,$\frac{{S}_{△ABC}}{{S}_{△BCD}}$的值为( )
如图,B、C两点都在反比例函数y=$\frac{k}{x}$(x>0)上,点A在y轴上,AB∥x轴,当△ABC是等边三角形时,$\frac{{S}_{△ABC}}{{S}_{△BCD}}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com