
【题目】如图,![]() ,
,![]() ,
,![]() 的平分线与
的平分线与![]() 的平分线交于点
的平分线交于点![]() ,则
,则![]() 的度数是________.
的度数是________.

【答案】![]()
【解析】
过点E作EG∥AB,过点F作FP∥AB,根据平行线的性质可得∠ABE+∠BEG=180°,∠GED+∠EDC=180°,根据角的计算以及角平分线的定义可得∠FBE+∠EDF=![]() (∠ABE+∠CDE),再依据∠ABF=∠BFP,∠CDF=∠DFP结合角的计算即可得出结论.
(∠ABE+∠CDE),再依据∠ABF=∠BFP,∠CDF=∠DFP结合角的计算即可得出结论.
解:如图,过点E作EG∥AB,过点F作FP∥AB,
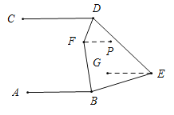
∵AB∥CD,
∴AB∥CD∥GE∥FP
∴∠ABE+∠BEG=180°,∠GED+∠EDC=180°,
∴∠ABE+∠CDE+∠BED=360°;
又∵∠BED=60°,
∴∠ABE+∠CDE=300°.
∵∠ABE和∠CDE的平分线相交于F,
∴∠ABF+∠CDF=![]() (∠ABE+∠CDE)=150°,
(∠ABE+∠CDE)=150°,
∵FP∥AB,AB∥CD,
∴AB∥CD∥FP,
∴∠ABF=∠BFP,∠CDF=∠DFP
∴∠BFD=∠BFP+∠DFP=∠ABF+∠CDF =150°.
故答案为:150°.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】下图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等。四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。

其中,你认为正确的见解有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
①若![]() 是完全平方式,则k=3
是完全平方式,则k=3
②工程建筑中经常采用三角形的结构,这是利用三角形具有稳定性的性质
③在三角形内部到三边距离相等的点是三个内角平分线的交点
④当![]() 时
时![]()
⑤若点P在∠AOB内部,D,E分别在∠AOB的两条边上,PD=PE,则点P在∠AOB的平分线上
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来交通事故发生率逐年上升,交通问题成为重大民生问题,鄱阳二中数学兴趣小组为检测汽车的速度设计了如下实验:如图,在公路MN(近似看作直线)旁选取一点C,测得C到公路的距离为30米,再在MN上选取A、B两点,测得∠CAN=30°,∠CBN=60°.
(1)求AB的长;(精确到0.1米,参考数据![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
(2)若本路段汽车限定速度为40千米/小时,某车从A到B用时3秒,该车是否超速?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,AC=BC,∠ACB=90°,过点C作CD⊥AB于点D,点E是AB边上一动点(不含端点A,B),连接CE,过点B作CE的垂线交直线CE于点F,交直线CD于点G.

(1)求证:AE=CG;
(2)若点E运动到线段BD上时(如图②),试猜想AE,CG的数量关系是否发生变化,请证明你的结论;
(3)过点A作AH⊥CE,垂足为点H,并交CD的延长线于点M(如图③),找出图中与BE相等的线段,直接写出答案BE=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如:![]() .我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如:
.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如:![]() ,
,![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如:![]() ,
,![]() 这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如:
这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如:![]() ;再如:
;再如:![]() .
.
解决下列问题:
(1)分式![]() 是_____分式(填“真分式”或“假分式”);
是_____分式(填“真分式”或“假分式”);
(2)把假分式![]() 化为带分式的形式(写出过程);
化为带分式的形式(写出过程);
(3)如果分式![]() 的值为整数,那么
的值为整数,那么![]() 的整数值为_____.
的整数值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF.
(1)如图1,∠EOF在直线CD的右侧:
①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)如图2,∠EOF在直线CD的左侧,且点E在点F的下方:
①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(8,6),C(0,10),AC=CO,直线AC交x轴于点M,将△AOC沿直线AC翻折,使得点O落在点B处,连接AB交x轴于D,动点P从点O出发,以2个单位长度/秒的速度沿射线OA运动;同时动点Q从A出发以每秒1个单位的速度沿射线AB运动。

(1)求B点的坐标;
(2)连接PB,设点P的运动时间为t秒,△PAB的面积为S,求S与t的关系式,并直接写t的取值范围;
(3)在点P、Q运动过程中,当t为何值时,△APQ是以PQ为底边的等腰三角形?并直接写出Q点坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() ,下面写出了说明“
,下面写出了说明“![]() ”的过程,请填空:
”的过程,请填空:

∵![]() ,
,![]()
∴![]() _______,
_______,![]() ________.(________________________)
________.(________________________)
∵![]()
∴![]() ___________,(________________________)
___________,(________________________)
∵![]()
∴![]() ___________,(________________________)
___________,(________________________)
∴![]() .(等量代换)
.(等量代换)
∵![]() (平角定义)
(平角定义)
∴![]() (等量代换)
(等量代换)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com