
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C. 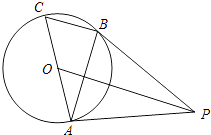
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
【答案】
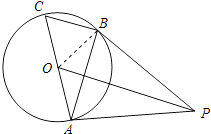
(1)证明:连接OB,如图所示:
∵AC是⊙O的直径,
∴∠ABC=90°,
∴∠C+∠BAC=90°,
∵OA=OB,
∴∠BAC=∠OBA,
∵∠PBA=∠C,
∴∠PBA+∠OBA=90°,
即PB⊥OB,
∴PB是⊙O的切线
(2)解:∵⊙O的半径为2 ![]() ,
,
∴OB=2 ![]() ,AC=4
,AC=4 ![]() ,
,
∵OP∥BC,
∴∠C=∠BOP,
又∵∠ABC=∠PBO=90°,
∴△ABC∽△PBO,
∴ ![]() ,
,
即 ![]() ,
,
∴BC=2
【解析】(1)连接OB,由圆周角定理得出∠ABC=90°,得出∠C+∠BAC=90°,再由OA=OB,得出∠BAC=∠OBA,证出∠PBA+∠OBA=90°,即可得出结论;(2)证明△ABC∽△PBO,得出对应边成比例,即可求出BC的长.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款. 乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔买水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=12cm,且![]() ,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
,BC=10cm,点D为AB的中点.如果点P在线段BC上以2cm/s的速度由点B向C点运动,同时,点Q在线段AC上由点A向C点以4cm/s的速度运动.
(1)若点P、Q两点分别从B、A两点同时出发,经过2秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点P、Q两点分别从B、A两点同时出发,△CPQ的周长为18cm,问:经过几秒后,△CPQ是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以AC,BC为边作等边△ACD和等边△BCE.设△ACD、△BCE、△ABC的面积分别是S1、S2、S3 , 现有如下结论:
①S1:S2=AC2:BC2;
②连接AE,BD,则△BCD≌△ECA;
③若AC⊥BC,则S1S2= ![]() S32 .
S32 .
其中结论正确的序号是 . 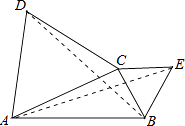
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以AC,BC为边作等边△ACD和等边△BCE.设△ACD、△BCE、△ABC的面积分别是S1、S2、S3 , 现有如下结论:
①S1:S2=AC2:BC2;
②连接AE,BD,则△BCD≌△ECA;
③若AC⊥BC,则S1S2= ![]() S32 .
S32 .
其中结论正确的序号是 . 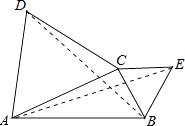
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=x-2y,B=-x-4y+1.
(1)求2(A+B)-(A-B);(结果用含x,y的代数式表示)
(2)当![]() 与
与![]() 互为相反数时,求(1)中代数式的值.
互为相反数时,求(1)中代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过反比例函数y=![]() (x>0)的图象上一点A作x轴的平行线,交双曲线y=-
(x>0)的图象上一点A作x轴的平行线,交双曲线y=-![]() (x<0)于点B,过B作BC∥OA交双曲线y=-
(x<0)于点B,过B作BC∥OA交双曲线y=-![]() (x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.
(x<0)于点D,交x轴于点C,连接AD交y轴于点E,若OC=3,求OE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com