

分析 (1)如图1中,延长FH交BC的延长线于M,由△FDH≌△MCH,推出FH=HM,再利用直角三角形斜边中线的性质即可解决问题.
(2)分两种情形①当FD=FH时,设∠M=∠DFH=x,构建方程解决问题.②当∠D=90°时,易知DF=DH,△DEF是等腰直角三角形.
解答 (1)证明:如图1中,延长FH交BC的延长线于M/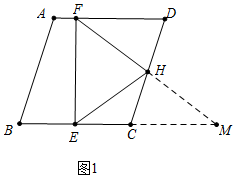
∵四边形ABCD是菱形,
∴AD∥BM,
∴∠DFH=∠M,
在△FDH和△MCH中,‘
$\left\{\begin{array}{l}{∠DFH=∠M}\\{∠FHD=∠CHM}\\{DH=HC}\end{array}\right.$,
∴△FDH≌△MCH,
∴FH=HM,
∵FE⊥BC,
∴∠FEM=90°,
∴EH=FH=HM,
∴EH=FH.
(2)解:如图2中,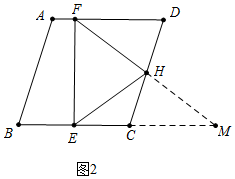
①当FD=FH时,设∠M=∠DFH=x,
∵BE=EC,CH=DH,BC=CD,
∴EC=CH,
∴∠CEH=∠CHE,
∵HE=HM,
∴∠CEH=∠CHE=∠M=x,
∴∠HCM=∠ECH+∠EHC=2x=∠D=∠FHD,
∵∠DFH+∠D+∠FHD=180°,
∴x+2x+2x=180°,
∴5x=180°,
∴x=36°,
∴∠D=72°.
②当∠D=90°时,易知DF=DH,△DEF是等腰直角三角形,
综上所述,当△DFH是等腰三角形时,∠D=72°或90°.
点评 本题考查矩形的性质、线段的垂直平分线的性质、等腰三角形的判定、直角三角形斜边中线定理等知识,解题的关键是学会分类讨论的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购票张数 | 1-50张 | 51~100张 | 100张以上 |
| 每张票价 | 13元 | 11元 | 9元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ②③ | B. | ①④ | C. | 只有③ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com