
【题目】如图,已知四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求四边形![]() 的面积
的面积![]() ;
;
(2)动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度,沿
出发,以每秒1个单位长度的速度,沿![]() 方向,向点
方向,向点![]() 运动;动点
运动;动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度,沿
出发,以每秒1个单位长度的速度,沿![]() 方向,向点
方向,向点![]() 运动,过点
运动,过点![]() 作
作![]() 于点
于点![]() .若
.若![]() 、
、![]() 两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为
两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为![]() .问:
.问:
①当点![]() 在
在![]() 上运动时,是否存在这样的
上运动时,是否存在这样的![]() ,使得直线
,使得直线![]() 将四边形
将四边形![]() 的周长平分?若存在,请求出
的周长平分?若存在,请求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
②在运动过程中,是否存在这样的![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出所有符合条件的
相似?若存在,请求出所有符合条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)40;(2)①当![]() 时,
时,![]() 将四边形
将四边形![]() 的周长平分.②
的周长平分.②![]() 或
或![]() 时,以
时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
【解析】
(1)作![]() 交
交![]() 于点
于点![]() ,利用勾股定理的逆定理证得四边形
,利用勾股定理的逆定理证得四边形![]() 是直角梯形,然后根据直角梯形的面积公式即可求得;
是直角梯形,然后根据直角梯形的面积公式即可求得;
(2)①利用周长平分,列出方程即可求解;
②当点P在AB上时,分![]() 和
和![]() 两种情况,根据等角的正切函数构建方程即可求解;当点P在AD和DC上时,不可能构成与
两种情况,根据等角的正切函数构建方程即可求解;当点P在AD和DC上时,不可能构成与![]() 相似的三角形.
相似的三角形.
(1)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() ;
;![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴四边形![]() 是直角梯形.
是直角梯形.
![]() .
.

(2)①当点![]() 在
在![]() 上运动时,
上运动时,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴当![]() 时,
时,![]() 将四边形
将四边形![]() 的周长平分.
的周长平分.
②∵![]() ,
,![]() ,
,![]() ,
,
∴点![]() 运动到
运动到![]() 时运动停止,
时运动停止,
∴![]() .
.
第一种情况:![]() ,若
,若![]() ,则
,则![]() .
.
∴![]() .
.
∴![]() ,∴
,∴![]() .
.
若![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
第二种情况:![]() ,
,![]() 、
、![]() 、
、![]() 三点不能组成三角形;
三点不能组成三角形;
第三种情况:![]() ,
,![]() 为钝角三角形与
为钝角三角形与![]() 不相似;
不相似;
∴![]() 或
或![]() 时,以
时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.


科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们县是紫菜生产大县,某景点商户向游客推销一种加工好的优质紫菜,已知每千克成本为20元.市场调查发现,在一段时间内,该产品销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)的变化而变化有如下关系式:
(元/千克)的变化而变化有如下关系式:![]() .设这种紫菜在这段时间内的销售利润为
.设这种紫菜在这段时间内的销售利润为![]() (元).
(元).
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定该景区这种紫菜的销售单价不得高于28元/千克,该商户每天能否获得比150元更大的利润?如果能请求出最大利润,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家刘徽发展了“重差术”,用于测量不可到达的物体的高度,比如,通过下列步骤可测量山的高度PQ(如图):
(1)测量者在水平线上的A处竖立一根竹竿,沿射线QA方向走到M处,测得山顶P、竹竿顶端B及M在一条直线上;
(2)将该竹竿竖立在射线QA上的C处,沿原方向继续走到N处,测得山顶P、竹竿顶端D及N在一条直线上;
(3)设竹竿与AM、CN的长分别为![]() 、a1、a2,可得公式:PQ=
、a1、a2,可得公式:PQ=![]() +
+![]() .则上述公式中,d表示的是( )
.则上述公式中,d表示的是( )
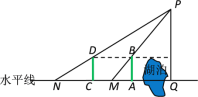
A. QA的长 B. AC的长 C. MN的长 D. QC的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物50元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在某一区域就可以获得该区域相对应的奖品.若恰巧落在两区域交界线上,则重新转动转盘.下表是活动进行中的一组统计数据:
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“矿泉水”的次数 | 68 | 111 | 136 | 345 | 564 | 701 |
假如你去转动该转盘一次,你获得牙膏的概率约是______.(用小数表示,结果保留一位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 6,AC = 8.点D是AB边上一点,过点D作DE // BC,交边AC于E.过点C作CF // AB,交DE的延长线于点F.
(1)如果![]() ,求线段EF的长;
,求线段EF的长;
(2)求∠CFE的正弦值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,求直径CD的长”.(1尺=10寸)则CD=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com