
【题目】如图,在![]() 中,
中,![]() 点
点![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 与点
与点![]() 不重合),过动点
不重合),过动点![]() 作
作![]() 交
交![]() 于点
于点![]()
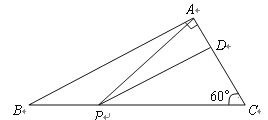
(1)若![]() 与
与![]() 相似,则
相似,则![]() 是多少度?
是多少度?
(2)试问:当![]() 等于多少时,
等于多少时,![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
(3)若以线段![]() 为直径的圆和以线段
为直径的圆和以线段![]() 为直径的圆相外切,求线段
为直径的圆相外切,求线段![]() 的长.
的长.
【答案】(1)60°或30°.(2)PC等于12时,![]() 的面积最大,最大面积是
的面积最大,最大面积是![]() .(3)
.(3)![]()
【解析】
(1)当△ABC与△DAP相似时,应有∠APD=∠B或∠APD=∠C,即∠APD为30°或60°.
(2)设PC=x,由PD∥BA,得∠BAC=∠PDC=90°,∴AC=BCcos60°=12,CD=xcos60°=![]() x,AD=12-
x,AD=12-![]() x,而PD=xsin60°=
x,而PD=xsin60°=![]() x,∴S△APD=
x,∴S△APD=![]() PDAD把PD,AD的值代入,得到S△APD=
PDAD把PD,AD的值代入,得到S△APD=![]() .∴PC等于12时,△APD的面积最大,最大面积是18
.∴PC等于12时,△APD的面积最大,最大面积是18![]() .
.
(3)设以BP和AC为直径的圆心分别为O1、O2,过O2作O2E⊥BC于点E,设⊙O1的半径为x,则BP=2x,AC=12,∴O2C=6,∴CE=6cos60°=3.∴由勾股定理得,O2E=![]() ,O1E=21-x,由于⊙O1和⊙O2外切,则圆心距O1O2=x+6.在Rt△O1O2E中,有O1O22=O2E2+O1E2,即(x+6)2=(21-x)2+(3
,O1E=21-x,由于⊙O1和⊙O2外切,则圆心距O1O2=x+6.在Rt△O1O2E中,有O1O22=O2E2+O1E2,即(x+6)2=(21-x)2+(3![]() )2,求解得到x的值,进而求得BP的值.
)2,求解得到x的值,进而求得BP的值.
(1)当△ABC与△DAP相似时,∠APD的度数是60°或30°.
(2)设![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,而
,而![]() ,
,
∴![]()
![]() .
.
∴PC等于12时,![]() 的面积最大,最大面积是
的面积最大,最大面积是![]() .
.
(3)设以![]() 和
和![]() 为直径的圆心分别为
为直径的圆心分别为![]() 、
、![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,
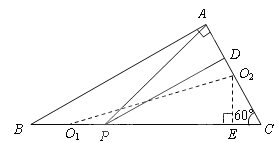
设![]() 的半径为
的半径为![]() ,则
,则![]() .显然,
.显然,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() 和
和![]() 外切,∴
外切,∴![]() .
.
在![]() 中,有
中,有![]() ,
,
∴![]() ,解得:
,解得:![]() , ∴
, ∴![]()


科目:初中数学 来源: 题型:
【题目】已知关于 x 的一元二次方程 x![]() 2k 1 x k
2k 1 x k![]() k 1 0 有实数根.
k 1 0 有实数根.
(1)求k 的取值范围;
(2)若此方程的两实数根![]() ,
,![]() 满足
满足![]()
![]() 11 ,求k 的值.
11 ,求k 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
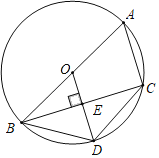
【题目】如图,四边形ABDC内接于⊙O,AB是⊙O的直径,OD⊥BC于点E.
(1)请你写出两个不相同的结论(不添加辅助线);
(2)连接AD,若BE=4,AC=6,求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网上书店以每本24元的价格购进了600本某种畅销书籍(定价每本45元),第一个月以每本36元销售,卖出了200本;第二个月书店为了增加销售量,决定在第一个月价格的基础上降价销售,根据市场调查,每本书每降低1元,可多售出20本,但最低售价应高于购进的价格.第二个月结束后,书店将剩余的书籍捐赠给某希望学校,设第二个月每本降低![]() 元.
元.

(1)填表:(列式,不需要化简)
时间 | 第一个月 | 第二个月 |
每本售价(元) | 36 | |
销售量(本) | 200 |
(2)如果该书店希望通过销售这批书籍获利2400元,那么第二个月每本书的售价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
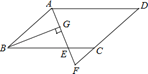
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=![]() ,则△CEF的面积是( )
,则△CEF的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )

A. 6![]() B. 10 C. 2
B. 10 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com