
����Ŀ�������ķ��ദ����������ã����Լ�����Ⱦ����ʡ��Դ��ij���л�������Ϊ������˴�ʵЧ�����������˲��־���С��һ��ʱ�������������ķ������������õ������������Ƴ�����������������ͳ��ͼ����ע��AΪ�ɻ����BΪ����������CΪ�к�������DΪ����������
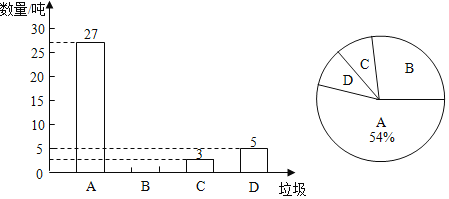
����ͳ��ͼ�ṩ����Ϣ������������⣺
��1������γ��������У�һ������ ���ֵ�����������
��2���뽫����ͳ��ͼ����������
��3������ͳ��ͼ�У�B����Ӧ�İٷֱ����� ����D����Ӧ��Բ�ĽǶ������� ����
��4������ó���ÿ�²�������������Ϊ5000�֣���ȫ�����ദ���������ÿ�²������к��������ٶ֣�
���𰸡���1��50����2�������������3��30%�� 36�㣻��4��500��
��������
��1��������ͳ��ͼ�пɵõ���A�ɻ�������������27�֣�ռ����������54%����������������������
��2�������B�ͳ������Ķ��������ɲ�ȫ����ͳ��ͼ��
��3��B�ͳ�������15��ռ��������50�ֵİٷֱȼ��ɣ�D�к�����ռ![]() �����Բ�Ľ�ռ360����
�����Բ�Ľ�ռ360����![]() ���ɣ�
���ɣ�
��4�������������壬������ϲ����D�к���������ռ![]() ����˹���5000�ֵ�
����˹���5000�ֵ�![]() �����к��������Ķ�����
�����к��������Ķ�����
��1��27��54%��50�֣�
�ʴ�Ϊ��50��
��2��50��27��3��5��15�֣���ȫ����ͳ��ͼ��ͼ��ʾ��
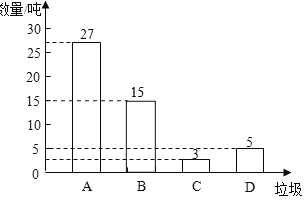
��3��15��50��30%��360���![]() ��36����
��36����
�ʴ�Ϊ��30%��36����
��4��5000��![]() ��500�֣�
��500�֣�
�𣺸ó���ÿ�²�����5000�������������к�����500�֣�


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �У�
��![]() ��
��![]() ��ֱ��
��ֱ��![]() �Ķ���P��BC���е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F����������������ۣ���
�Ķ���P��BC���е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F����������������ۣ���![]() ����
����![]() �ǵ���ֱ�������Σ���
�ǵ���ֱ�������Σ���![]() ����
����![]() ����
����![]() ��������ȷ���У� ��
��������ȷ���У� ��
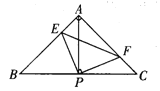
A.2��B.3��C.4��D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
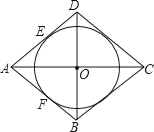
����Ŀ����ͼ����֪��O�������ABD������AB��AD�ֱ������ڵ�E��F������AO���ӳ�����C��ʹOC=AO������CD��CB��
��1�����ж��ı���ABCD����״����˵�����ɣ�
��2����AB=4cm����գ�
�ٵ���O�İ뾶Ϊ ��cmʱ����ABDΪ�ȱ������Σ�
�ڵ���O�İ뾶Ϊ�� ��cmʱ���ı���ABCDΪ�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=mx+n��m��0����ͼ���뷴��������y=![]() ��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����ΪM��BM=OM��OB=2
��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����ΪM��BM=OM��OB=2![]() ����A��������Ϊ4��
����A��������Ϊ4��
��1����÷�����������һ�κ����Ľ���ʽ��
��2������MC�����ı���MBOC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ҹ��غ���һ�Ҳ����������ִ������ҹ�����,�Һ����ס�������Ѳ��ͧ���������13nmile��A��B��������ǰȥ���أ������Ӻ�ͬʱ����C�ؽ������أ���֪��Ѳ��ͧÿСʱ����120nmile����Ѳ��ͧÿСʱ����50nmile������Ϊ��ƫ��40�������Ѳ��ͧ�ĺ���
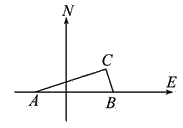
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�AB=AC����BAC=90
�У�AB=AC����BAC=90![]() ��ֱ�ǡ�EPF�Ķ�����BC���е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F����������������ۣ���1��AE=CF����2����APE =��CPF����3����EPF�ǵ���ֱ�������Σ���4��
��ֱ�ǡ�EPF�Ķ�����BC���е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F����������������ۣ���1��AE=CF����2����APE =��CPF����3����EPF�ǵ���ֱ�������Σ���4��![]() =
=![]()
![]() ��5��EF=AP����һ����������________����
��5��EF=AP����һ����������________����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ƻ�����һ�������������֪����2�������1��������320Ԫ������3�������2��������540Ԫ��
��1����ÿ�������ÿ��������ۼۣ�
��2�����ѧУ�ƻ�������������50�����ܷ��ò�����5500Ԫ����ô���ɹ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6��С������ֽƬ����ͼ1��ʾ����ͼ2��ʾ�ķ�ʽ���ص��ķ��ڳ�����ABCD�ڣ�δ�����ǵIJ���ǡ�÷ָ�Ϊ���������Σ�����ֱ�ΪS1��S2����֪С������ֽƬ�ij�Ϊa����Ϊb����a>b����AB���Ȳ����BC�䳤ʱ����6��С������ֽƬ������ͬ���ķ�ʽ�����µij�����ABCD�ڣ�S1��S2�IJ��ܱ��ֲ��䣬��a��b����Ĺ�ϵ��

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ��֪��ABC��90�㣬��PΪ����BC������һ��(��P���B���غ�)���ֱ���AB��APΪ���ڡ�ABC���ڲ����ȱߡ�ABE�͡�APQ������QE���ӳ���BP�ڵ�F. ��˵������1����ABP�ա�AEQ����2��EF��BF
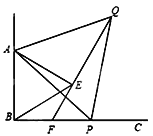
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com