
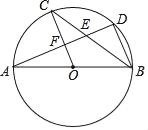
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD与BC,OC分别相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤△CEF≌△BED.其中一定成立的结论是_____.(填序号)
【答案】①③④
【解析】
①由直径所对圆周角是直角,
②由于∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,
③由平行线得到∠OCB=∠DBC,再由同圆的半径相等得到结论判断出∠OBC=∠DBC;
④用半径垂直于不是直径的弦,必平分弦;
⑤得不到△CEF和△BED中对应相等的边,所以不一定全等.
①∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
故①正确;
②∵∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,
∴∠AOC≠∠AEC,
故②不正确;
③∵OC∥BD,
∴∠OCB=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠DBC,
∴BC平分∠ABD,
故③正确;
④∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
∵OC∥BD,
∴∠AFO=90°,
∵点O为圆心,
∴AF=DF,
故④正确;
⑤∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不全等,
故⑤不正确;
综上可知:其中一定成立的有①③④,
故答案为:①③④.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
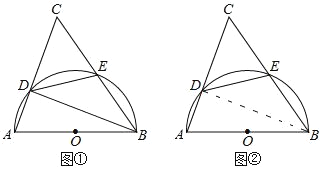
【题目】已知,△ABC中,∠A=68°,以AB为直径的⊙O与AC,BC的交点分别为D,E
(Ⅰ)如图①,求∠CED的大小;
(Ⅱ)如图②,当DE=BE时,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和图2,![]() 是直线
是直线![]() 上一动点,
上一动点,![]() 两点在直线
两点在直线![]() 的同侧,且点
的同侧,且点![]() 所在直线与
所在直线与![]() 不平行.
不平行.

(1)当![]() 点运动到
点运动到![]() 位置时,距离
位置时,距离![]() 点最近,在图1中的直线
点最近,在图1中的直线![]() 上画出点
上画出点![]() 的位置;
的位置;
(2)当![]() 点运动到
点运动到![]() 位置时,与
位置时,与![]() 点的距离和与
点的距离和与![]() 点距两相等,请在图2中作出
点距两相等,请在图2中作出![]() 位置;
位置;
(3)在直线![]() 上是否存在这样一点
上是否存在这样一点![]() ,使得到
,使得到![]() 点的距离与到
点的距离与到![]() 点的距离之和最小?若存在请在图3中作出这点,若不存在清说明理由.
点的距离之和最小?若存在请在图3中作出这点,若不存在清说明理由.
(要求:不写作法,请保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
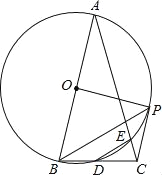
【题目】如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.
(1)BD=DC吗?说明理由;
(2)求∠BOP的度数;
(3)求证:CP是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
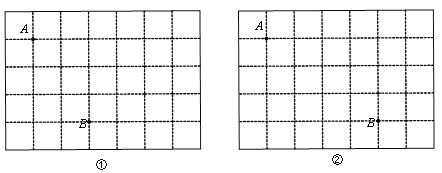
【题目】如图①、图②,方格纸中的每个小正方形的边长均为1,小正方形的顶点称为格点,图①和图②中的点A、点B都是格点.分别在图①、图②中画出格点C,并满足下面的条件:
(1)在图①中,使∠ABC=90°.此时AC的长度是 .
(2)在图②中,使AB=AC.此时△ABC的边AB上的高是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
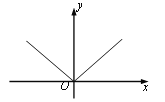
【题目】数学概念:百度百科上这样定义绝对值函数:y=│x│=![]()
并给出了函数的图像(如图).
方法迁移
借鉴研究正比例函数y=kx与一次函数y=kx+b(k,b是常数,且k≠0)之间关系的经验,我们来研究函数y=│x+a│(a是常数)的图像与性质.
“从‘1’开始”
我们尝试从特殊到一般,先研究当a=1时的函数y=│x+1│.
按照要求完成下列问题:
(1)观察该函数表达式,直接写出y的取值范围;
(2)通过列表、描点、画图,在平面直角坐标系中画出该函数的图像.
“从‘1’到一切”
(3)继续研究当a的值为-2,-![]() ,2,3,…时函数y=│x+a│的图像与性质,
,2,3,…时函数y=│x+a│的图像与性质,
尝试总结:
①函数y=│x+a│(a≠0)的图像怎样由函数y=│x│的图像平移得到?
②写出函数y=│x+a│的一条性质.
知识应用
(4)已知A(x1,y1),B(x2,y2)是函数y=│x+a│的图像上的任意两点,且满足x1<x2≤-1时, y1>y2,则a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校甲、乙两名同学去爱国主义教育基地参观,该基地与学校相距2400米.甲从学校步行去基地,出发5分钟后乙再出发,乙从学校骑自行车到基地. 乙骑行到一半时,发现有东西忘带,立即返回,拿好东西之后再从学校出发.在骑行过程中,乙的速度保持不变,最后甲、乙两人同时到达基地. 已知,乙骑行的总时间是甲步行时间的![]() .设甲步行的时间为
.设甲步行的时间为![]() (分),图中线段OA表示甲离开学校的路程
(分),图中线段OA表示甲离开学校的路程![]() (米)与
(米)与![]() (分)的函数关系的图像.图中折线B—C—D和线段EA表示乙离开学校的路程
(分)的函数关系的图像.图中折线B—C—D和线段EA表示乙离开学校的路程![]() (米)与
(米)与![]() (分)的函数关系的图像.根据图中所给的信息,解答下列问题:
(分)的函数关系的图像.根据图中所给的信息,解答下列问题:
(1)甲步行的速度和乙骑行的速度;
(2)甲出发多少时间后,甲、乙两人第二次相遇?
(3)若![]() (米)表示甲、乙两人之间的距离,当
(米)表示甲、乙两人之间的距离,当![]() 时,求
时,求![]() (米)关于
(米)关于![]() (分)的函数关系式.
(分)的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售10kgA级别和20kgB级别茶叶的利润为4000元,销售20kgA级别和10kgB级别茶叶的利润为3500元.
(1)求每千克A级别茶叶和B级别茶叶的销售利润;
(2)若该经销商一次购进两种级别的茶叶共200kg用于出口,其中B级别茶叶的进货量不超过A级别茶叶的2倍,请你帮该经销商设计一种进货方案使销售总利润最大,并求出总利润的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com