
分析 (1)根据“销售单价每涨2元,月销售量就减少20千克”,可知:月销售量=500-(销售单价-50)×$\frac{20}{2}$.由此可得出售价为55元/千克时的月销售量,然后根据利润=每千克的利润×销售的数量来求出月销售利润;
(2)销售成本不超过10000元,即进货不超过10000÷40=250kg.根据利润表达式求出当利润是8000时的售价,从而计算销售量,与进货量比较得结论.
解答 解:(1)当销售单价定为每千克55元时,月销售量为:500-(55-50)×10=450(千克),
所以月销售利润为:(55-40)×450=6750元;
(2)由于水产品不超过10000÷40=250kg,定价为x元,
则(x-40)[500-10(x-50)]=8000,
解得:x1=80,x2=60.
当x1=80时,进货500-10(80-50)=200kg<250kg,符合题意,
当x2=60时,进货500-10(60-50)=400kg>250kg,舍去.
答:商品想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应为80元.
点评 本题主要考查了一元二次方程的应用,能正确表示出月销售量是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在△ACD和△ABE中,CD与BE交于点O,下列三个说明:
如图,在△ACD和△ABE中,CD与BE交于点O,下列三个说明:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
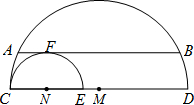 如图,CD为大半圆M的直径,E为CM上一点,以CE为直径画小半圆N,大半圆M的弦AB与小半圆N相切于点F,且AB∥CD,AB=4,设$\widehat{CD}$、$\widehat{CE}$的长分别为x、y,线段ED的长为z,则z(x+y)的值为8π.
如图,CD为大半圆M的直径,E为CM上一点,以CE为直径画小半圆N,大半圆M的弦AB与小半圆N相切于点F,且AB∥CD,AB=4,设$\widehat{CD}$、$\widehat{CE}$的长分别为x、y,线段ED的长为z,则z(x+y)的值为8π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com