
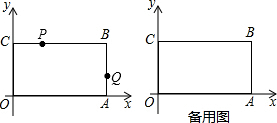
分析 (1)先用t表示出P、Q两点的坐标,再由反比例函数图象上点的坐标特点即可得出结论;
(2)先根据OQ垂直平分AP得出OP=OA,求出t的值,再由PQ=QA即可得出a的值;
(3)分∠OPQ=90°与∠POQ=90°两种情况进行分类讨论.
解答 解:(1)∵A(10,0),C(0,8),点P在边BC上以每秒1个单位长的速度由点C向点B运动,同时点Q在边AB上以每秒a个单位长的速度由点A向点B运动,
∴P(t,8),Q(10,at),
∵反比例函数y=$\frac{m}{x}$图象经过P点、Q点,
∴8t=10at,解得a=$\frac{4}{5}$;
(2)∵OQ垂直平分AP,
∴OP=OA,PQ=QA,
∴$\sqrt{{t}^{2}+{8}^{2}}$=10,解得t=6,
∴Q(10,6a),P(6,8),
∵PQ=QA,
∴(10-6)2+(6a-8)2=(6a)2,解得a=$\frac{5}{6}$;
(3)如图,
∵Q为AB的中点,
∴Q(10,4),P(t,8).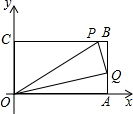
当∠OPQ=90°时,OP2+PQ2=OQ2,即t2+82+(10-t)2+42=102+42,整理得,t2-10t+32=0,
∵△=(-10)2-4×32=100-128=-28<0,
∴此方程无解,即此种情况不存在;
当∠POQ=90°时,OQP2+PQ2=OP2,即102+42+(10-t)2+42=t2+82,整理得,-20t=-168,解得t=$\frac{42}{5}$,
∵AQ=4,
∴at=4,即$\frac{42}{5}$a=4,解得a=$\frac{10}{21}$.
点评 本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点、直角三角形的判定与性质等知识,在解答(3)时要注意进行分类讨论.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
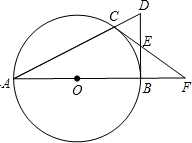 如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.
如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (6a9)÷(3a3)=2a3 | B. | (-4x3y)÷(2x2y)=-2x | C. | (x-y)3÷(y-x)=(y一x)2 | D. | am÷an÷ap=am-n+p |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com