
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD ≌△ACE ;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.

【答案】(1)证明见解析;(2)BD2+FC2=DF2,理由见解析;(3)![]() .
.
【解析】
(1)根据垂直的定义以及直角,得到∠BAD=∠CAE,然后SAS证明即可;
(2)根据等腰直角三角形的性质得到∠B=∠ACB=45°,然后由(1)的结论得到∠ACE=45°,BD=CE,从而得到∠FCE=90°,根据勾股定理得出![]() ,再根据SAS证明△DAF≌△EAF,根据全等三角形的性质得到DF=FE,从而得到结论;
,再根据SAS证明△DAF≌△EAF,根据全等三角形的性质得到DF=FE,从而得到结论;
(3)过点A作![]() 于G,根据(2)的结论得到DF=5,然后根据等腰直角三角形的性质求出DG,最后根据勾股定理求解即可.
于G,根据(2)的结论得到DF=5,然后根据等腰直角三角形的性质求出DG,最后根据勾股定理求解即可.
(1)∵![]()
∴![]()
又∵![]()
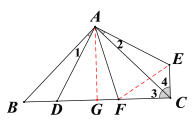
∴![]()
在△ABD和△ACE中
∴△ABD≌△ACE;
(2)![]() 理由如下:
理由如下:
连接FE, ∵![]()
∴![]()
由(1)知△ABD≌△ACE
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵AF平分![]()
∴![]()
在△DAF和△EAF中
∴△DAF≌△EAF
∴![]() .
.
∴![]() ;
;
(3)过点A作![]() 于G
于G
由(2)知![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴在![]() 中
中![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC的三个角是∠A,∠B,∠C ,它们所对的边分别是a,b,c.①c2-a2=b2;②∠A=![]() ∠B=
∠B=![]() ∠C;③c=
∠C;③c=![]() a=
a=![]() b;④a=2,b=2
b;④a=2,b=2 ![]() ,c=
,c=![]() .上述四个条件中,能判定△ABC 为直角三角形的有( )
.上述四个条件中,能判定△ABC 为直角三角形的有( )
A. 1个 B. 2个
C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在东西方向的海岸线MN上有A,B两港口,海上有一座小岛P,渔民每天都乘轮船从A,B 两港口沿AP,BP的路线去小岛捕鱼作业.已知小岛P在A港的北偏东60°方向,在B港的北偏西45°方向,小岛P距海岸线MN的距离为30海里.
(1)求AP,BP的长(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2);
≈2.2);
(2)甲、乙两船分别从A,B两港口同时出发去小岛P捕鱼作业,甲船比乙船晚到小岛24分钟.已知甲船速度是乙船速度的1.2倍,利用(1)中的结果求甲、乙两船的速度各是多少海里/时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,剪两张对边平行的纸片随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠DAB+∠ABC=180° B. AB=BC
C. AB=CD,AD=BC D. ∠ABC=∠ADC,∠BAD=∠BCD
查看答案和解析>>
科目:初中数学 来源: 题型:
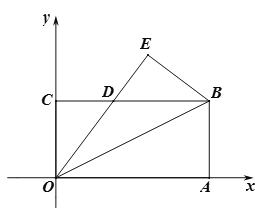
【题目】如图,矩形OABC的边OA,OC分别与坐标轴重合,并且点B的坐标为![]() .将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
.将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
(1)求证:△OBD为等腰三角形;
(2)求点E的坐标;
(3)坐标平面内是否存在一点F,使得以点B,E,F,O为顶点的四边形是平行四边形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y1=2x+3与直线l2:y2=kx﹣1相交于点A,A横坐标为﹣1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
(1)求出A点的坐标及直线l2的解析式;
(2)连接BC,求出S△ABC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com