
【题目】学农期间我们完成了每日一题,进一步研究了角的平分线. 工人师傅常用角尺平分一个任意角. 作法如下:
如图,∠AOB 是一个任意角,在边 OA、OB 上分别取 OM=ON, 移动角尺,使角尺两边相同的刻度分别与 M、N 重合. 过角尺顶点 C 的射线 OC 便是∠AOB 的平分线. 我们发现利用 SSS 证明两个三角形全等,从而证明∠AOC=∠BOC.

学习了轴对称的知识后,我们知道角是轴对称图形,角平分线 所在直线就是它的对称轴,爱动脑筋的小慧同学利用轴对称图形的性质发现了一种画角平分线的方法.
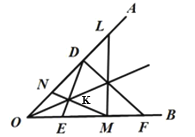
方法如下:如图 1,将两个全等的三角形纸片△DEF 和△MNL 的一组对应边分别与∠AOB 的一边共线,同时这条边所对顶点落在∠AOB 的另一条边上,则△DEF 和△MNL 的另一组对应边的交点 P 在∠AOB 的平分线上.

(1)小慧的做法正确吗?说明理由:
小旭说:利用轴对称的性质,我只用刻度尺就可以画角平分线.(提示:刻度尺可以度量出相等的线段)
(2)请你和小旭一样,只用刻度尺画出图 2 中∠QRS 的角平分线.(保留作图痕迹,不写作法)
【答案】(1)正确,证明见解析(2)图见解析.
【解析】
(1)说法正确,可通过用AAS证明三角形OED与三角形OME全等得到ON=OE,OD=OM,∠ODE=∠ONM,再根据DO-ON=OM-OE,得到DN=ME,再根据AAS证明三角形NKD与三角形EKM全等,得到NK=EK,再根据SAS证明三角形ONK与三角形OEK全等,从而得到对应角∠NOK=∠EOK,即可证明角平分线.
(2)根据(1)可知,作三角形RAD与三角形RBC全等,过R点作与BC与AD的交点的射线即为角平分线.
(1)正确.理由如下
∵![]()
∴∠DEF=∠MNL,DE=NM
∴180°-∠DEF=180°-∠MNL
即∠OED=∠ONM
在三角形OED与三角形ONM中
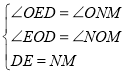
∴![]() (AAS)
(AAS)
∴ON=OE,OD=OM,∠ODE=∠OMN
∴DO-ON=OM-OE
即DN=ME
在三角形NKD与三角形EKM中

∴![]() (AAS)
(AAS)
∴NK=EK
在三角形ONK与三角形OEK中

∴![]() (SAS)
(SAS)
∴∠NOK=∠EOK
即OK为∠LOF 的角平分线.
(2)
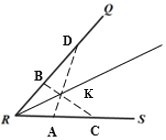
如图量RA=RA,RQ=RC,连接AD=BC.
则在三角形RAD与三角形RBC中

∴![]() (SAS)
(SAS)
∴∠RDA=∠RCB
在三角形BDK与三角形ACK中
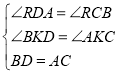
∴![]() (AAS)
(AAS)
∴BK=AK
在三角形RBK与三角形RAK中
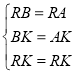
∴![]() (SSS)
(SSS)
∴∠BRK=∠ARK
故RK为角平分线.


科目:初中数学 来源: 题型:
【题目】5月份,某品牌衬衣正式上市销售.5月1日的销售量为10件,5月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到5月31日销售量为0.设该品牌衬衣的日销量为p(件),销售日期为n(日),p与n之间的关系如图所示.
(1)写出p关于n的函数关系式p= (注明n的取值范围);
(2)经研究表明,该品牌衬衣的日销量超过150件的时间为该品牌衬衣的流行期.请问:该品牌衬衣本月在市面的流行期是多少天?
(3)该品牌衬衣本月共销售了 件.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
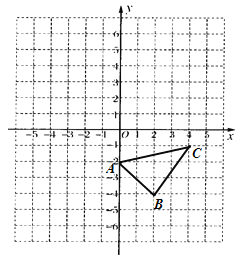
【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标:
三个顶点的坐标: ![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)直接写出△ABC的面积为 ;
(3)在![]() 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函双y=![]() (m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=
(m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=![]() ,OA=2.
,OA=2.
(1)求反比例函数和一次函数的解析式;
(2)点D是反比例函数图象在第三象限部分上的一点,且到x轴的距离是3,连接AD、BD,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=![]() .例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=
.例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= ![]() .
.
(1)若F(a)=![]() 且a为100以内的正整数,则a=________;
且a为100以内的正整数,则a=________;
(2)如果m是一个两位数,那么试问F(m)是否存在最大值或最小值?若存在,求出最大(或最小)值以及此时m的取值并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是反比例函数y=![]() 的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC使点C落在第二象限,且边BC交x轴于点D,若△ACD与△ABD的面积之比为1:2,则点C的坐标为( )
的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC使点C落在第二象限,且边BC交x轴于点D,若△ACD与△ABD的面积之比为1:2,则点C的坐标为( )

A. (﹣3,2![]() ) B. (﹣5,
) B. (﹣5,![]() ) C. (﹣6,
) C. (﹣6,![]() ) D. (﹣3
) D. (﹣3![]() ,2)
,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E、F分别在BC、CD上,将△ABE沿AE折叠,使点B落在AC上的点Bˊ处,又将△CEF沿EF折叠,使点C落在射线EBˊ与AD的交点Cˊ处,则![]() 的值( )
的值( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料
勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.

先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到![]() ,
,
整理,得![]() .
.
所以![]() .
.
如果把图1中的四个全等的直角三角形摆成图2所示的正方形,
请你参照上述证明勾股定理的方法,完成下面的填空:
由图2可以得到 ,
整理,得 ,
所以 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com