
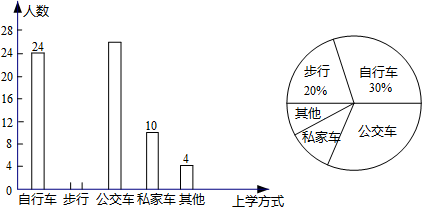
分析 (1)根据自行车所占比例为30%,而由条形图知一共有24人骑自行车上学,从而求出总人数;
(2)由扇形统计图知:步行占20%,而由(1)总人数已知,从而求出步行人数,补全条形图;
(3)根据被调查的总人数及自行车、步行、私家车、其他交通工具的人数可得乘公交车上学的人数,用样本中公交车上学人数所占比例乘以总人数1600即可得答案.
解答 解:(1)24÷30%=80,
答:一共抽取80人;
(2)“步行”的人数为:80×20%=16(人),
补全图,如下: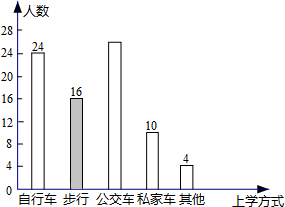
(3)∵乘公交车上学的人有80-(24+16+10+4)=26(人),
∴$\frac{26}{80}$×1600=520,
答:大约有520人乘坐公交.
点评 此题考查了条形统计图和扇形统计图及用样本估计总体,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知点P是正方形ABCD边AD上的一个动点,AE⊥BP,CF⊥BP,垂足点分別为点E,F,AD=4.PM∥FC交DC于M点
已知点P是正方形ABCD边AD上的一个动点,AE⊥BP,CF⊥BP,垂足点分別为点E,F,AD=4.PM∥FC交DC于M点 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,先将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A1B1C1.
如图,先将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
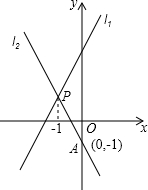 如图,直线l1与l2相交于点P,l1的解析式为y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).
如图,直线l1与l2相交于点P,l1的解析式为y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=3 | B. | x=0 | C. | x=2 | D. | x=a |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A、B在反比例函数y=$\frac{4}{x}$(x>0)的图象上,过点A、B作x轴的垂线,垂足分别为C、D,延长线段AB交x轴于点E,若OC=CD=DE,则△AOE的面积为6.
如图,点A、B在反比例函数y=$\frac{4}{x}$(x>0)的图象上,过点A、B作x轴的垂线,垂足分别为C、D,延长线段AB交x轴于点E,若OC=CD=DE,则△AOE的面积为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com