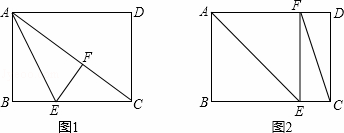
矩形纸片ABCD中，已知AD=8，AB=6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为
3或6 ．
解：①∠EFC=90°时，如图1，
∵∠AFE=∠B=90°，∠EFC=90°，
∴点A、F、C共线，
∵矩形ABCD的边AD=8，
∴BC=AD=8，
在Rt△ABC中，AC=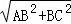
=
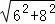=10，
设BE=x，则CE=BC﹣BE=8﹣x，
由翻折的性质得，AF=AB=6，EF=BE=x，
∴CF=AC﹣AF=10﹣6=4，
在Rt△CEF中，EF2+CF2=CE2，
即x2+42=（8﹣x）2，
解得x=3，
即BE=3；
②∠CEF=90°时，如图2，
由翻折的性质得，∠AEB=∠AEF=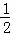
×90°=45°，
∴四边形ABEF是正方形，
∴BE=AB=6，
综上所述，BE的长为3或6．
故答案为：3或6．
科目：初中数学 来源： 题型：
如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上．若AB=6，BC=9，则BF的长为（ ）
|
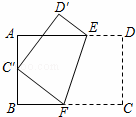
| A． | 4 | B． | 3 | C． | 4.5 | D． | 5 |
查看答案和解析>>
科目：初中数学 来源： 题型：
数学问题：计算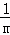
+
+
+…+
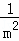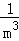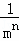（其中m，n都是正整数，且m≥2，n≥1）．
探究问题：为解决上面的数学问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算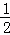
+
+
+…+
．
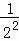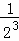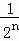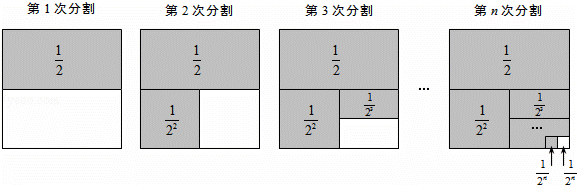
第1次分割，把正方形的面积二等分，其中阴影部分的面积为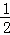
；
第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为+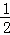
；
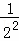第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为++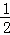
+…+
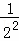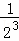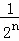，最后空白部分的面积是．
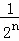根据第n次分割图可得等式：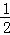
+
+
+…+
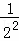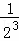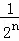=1﹣．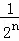
探究二：计算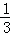
+
+
+…+
．
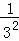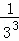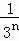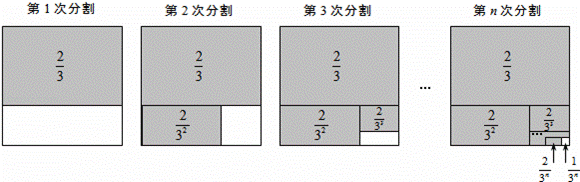
第1次分割，把正方形的面积三等分，其中阴影部分的面积为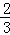
；
第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为+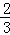
；
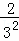第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为++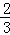
+…+
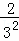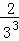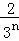，最后空白部分的面积是
．
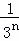根据第n次分割图可得等式：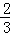
+
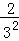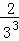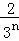++…+=1﹣，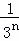
两边同除以2，得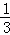
+
+
+…+
=
﹣
．
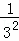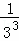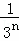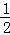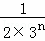探究三：计算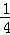
+
+
+…+
．
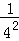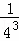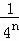（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）
解决问题：计算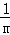
+
+
+…+
．
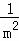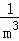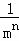（只需画出第n次分割图，在图上标注阴影部分面积，并完成以下填空）
根据第n次分割图可得等式：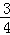 
+
+
+…+
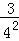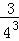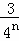=1﹣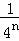
，
所以，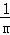
+
+
+…+
= 
﹣
．
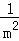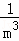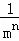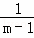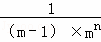拓广应用：计算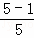 
+
+
+…+
．
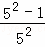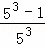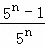查看答案和解析>>
科目：初中数学 来源： 题型：
如图，过点O作直线与双曲线y=
（k≠0）交于A、B两点，过点B作BC⊥x轴于点C，作BD⊥y轴于点D．在x轴上分别取点E、F，使点A、E、F在同一条直线上，且AE=AF．设图中矩形ODBC的面积为S1，△EOF的面积为S2，则S1、S2的数量关系是（ ）
|
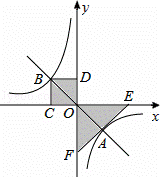
| A． | S1=S2 | B． | 2S1=S2 | C． | 3S1=S2 | D． | 4S1=S2 |
查看答案和解析>>
科目：初中数学 来源： 题型：
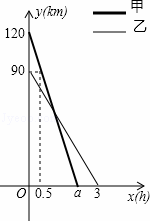
在一条笔直的公路旁依次有A、B、C三个村庄，甲、乙两人同时分别从A、B两村出发，甲骑摩托车，乙骑电动车沿公路匀速驶向C村，最终到达C村．设甲、乙两人到C村的距离y1，y2（km）与行驶时间x（h）之间的函数关系如图所示，请回答下列问题：
（1）A、C两村间的距离为 km，a= ；
（2）求出图中点P的坐标，并解释该点坐标所表示的实际意义；
（3）乙在行驶过程中，何时距甲10km？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（k＞0）的图象上，则y1 y2（填“＞”“＜”或“=”）
