
已知抛物线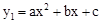 a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:
a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:
|
x |
… |
―1 |
0 |
3 |
… |
|
|
… |
0 |
|
0 |
… |
(1)求y1与x之间的函数关系式;
(2)若经过点T(0,t)作垂直于y轴的直线l′,A为直线l′上的动点,线段AM的垂直平分线交直线l于点B,点B关于直线AM的对称点为P,记P(x,y2).
①求y2与x之间的函数关系式;
②当x取任意实数时,若对于同一个x,有y1<y2恒成立,求t的取值范围.
解:(1)∵抛物线经过点(0,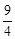 ),∴c=
),∴c=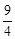 。∴
。∴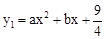 。
。
∵点(-1,0)、(3,0)在抛物线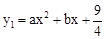 上,
上,
∴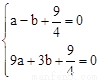 ,解得
,解得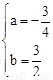 。
。
∴y1与x之间的函数关系式为: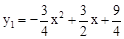 。
。
(2)∵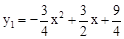 ,∴
,∴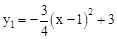 。
。
∴直线l为x=1,顶点M(1,3).
①由题意得,t≠3,
如图,记直线l与直线l′交于点C(1,t),
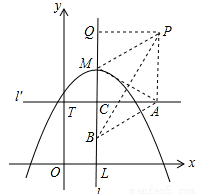
当点A′与点C不重合时,
∵由已知得,AM与BP互相垂直平分,
∴四边形ANMP为菱形。∴PA∥l。
又∵点P(x,y2),∴点A(x,t)(x≠1)。∴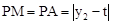 。
。
过点P作PQ⊥l于点Q,则点Q(1,y2),∴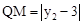 ,
,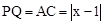 。
。
在Rt△PQM中,∵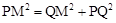 ,即
,即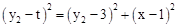 。
。
整理得,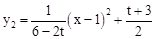 ,即
,即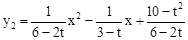 。
。
当点A与点C重合时,点B与点P重合,
∴P(1,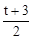 )。∴P点坐标也满足上式。
)。∴P点坐标也满足上式。
∴y2与x之间的函数关系式为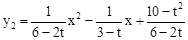 (t≠3)。
(t≠3)。
②根据题意,借助函数图象:
当抛物线y2开口方向向上时,6-2t>0,即t<3时,抛物线y1的顶点M(1,3),抛物线y2的顶点(1,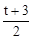 ),
),
∵3>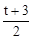 ,∴不合题意。
,∴不合题意。
当抛物线y2开口方向向下时,6-2t<0,即t>3时,
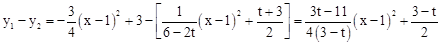 ,
,
若3t-11≠0,要使y1<y2恒成立,只要抛物线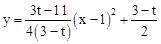 开口方向向下,且顶点(1,
开口方向向下,且顶点(1,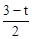 )在x轴下方,
)在x轴下方,
∵3-t<0,只要3t-11>0,解得t>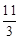 ,符合题意。
,符合题意。
若3t-11=0,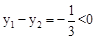 ,即t=
,即t=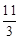 也符合题意。
也符合题意。
综上所述,可以使y1<y2恒成立的t的取值范围是t≥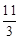 。
。
【解析】
试题分析:(1)先根据物线经过点(0,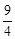 )得出c的值,再把点(-1,0)、(3,0)代入抛物线y1的解析式即可得出y1与x之间的函数关系式。
)得出c的值,再把点(-1,0)、(3,0)代入抛物线y1的解析式即可得出y1与x之间的函数关系式。
(2)先根据(I)中y1与x之间的函数关系式得出顶点M的坐标.
①记直线l与直线l′交于点C(1,t),当点A′与点C不重合时,由已知得,AM与BP互相垂直平分,故可得出四边形ANMP为菱形,所以PA∥l,再由点P(x,y2)可知点A(x,t)(x≠1),所以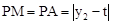 ,过点P作PQ⊥l于点Q,则点Q(1,y2),故
,过点P作PQ⊥l于点Q,则点Q(1,y2),故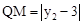 ,
,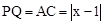 ,在Rt△PQM中,根据勾股定理即可得出y2与x之间的函数关系式,再由当点A与点C重合时,点B与点P重合可得出P点坐标,故可得出y2与x之间的函数关系式。
,在Rt△PQM中,根据勾股定理即可得出y2与x之间的函数关系式,再由当点A与点C重合时,点B与点P重合可得出P点坐标,故可得出y2与x之间的函数关系式。
②据题意,借助函数图象:
当抛物线y2开口方向向上时,可知6-2t>0,即t<3时,抛物线y1的顶点M(1,3),抛物线y2的顶点(1,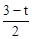 ),由于3>
),由于3>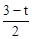 ,所以不合题意。
,所以不合题意。
当抛物线y2开口方向向下时,6-2t<0,即t>3时,求出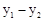 的值。若3t--11≠0,要使y1<y2恒成立,只要抛物线
的值。若3t--11≠0,要使y1<y2恒成立,只要抛物线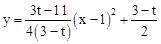 方向向下及且顶点(1,
方向向下及且顶点(1,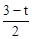 )在x轴下方,因为3-t<0,只要3t-11>0,解得t>
)在x轴下方,因为3-t<0,只要3t-11>0,解得t>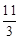 ,符合题意;若3t-11=0,
,符合题意;若3t-11=0,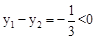 ,即t=
,即t=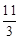 也符合题意。
也符合题意。


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
 正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为
正半轴交于点C.如果x1、x2是方程x2-x-6=0的两个根(x1<x2),且△ABC的面积为| 15 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为y=-| 1 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| c | a |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com