
 ��3����E��
��3����E�� ��0����ԭ��O��0��0��
��0����ԭ��O��0��0��

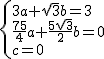
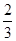 ��b=
��b= ��c=0��
��c=0��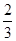 x2+
x2+ x��
x��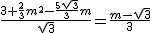
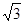 ��m2=
��m2=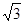 ��
��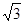 ʱ��n=2����ΪP�㣬
ʱ��n=2����ΪP�㣬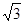 ��2��
��2�� ��
��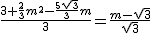
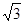 ��m2=
��m2=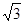 ��
��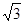 ʱ����ΪP�㣬
ʱ����ΪP�㣬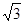 ʱ��n=-3��
ʱ��n=-3��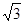 ��-3����
��-3����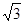 ��2������3
��2������3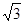 ��-3����
��-3����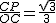
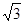 ��2��ʱ����BPQ=��COP=30�ȣ�
��2��ʱ����BPQ=��COP=30�ȣ�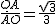 ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
������12�֣���֪���κ�����ͼ���㣨0��-3�����Ҷ�������Ϊ��-1��-4��.
��1����ö��κ����Ľ���ʽ��
��2����ö��κ�����ͼ����x��Ľ���ΪA��B����y��Ľ���ΪC�����ABC�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�꽭��ʡ��������ѧ�п�ģ�⿼����ѧ��.doc ���ͣ������
��������12�֣���֪���κ���y=x2��bx��c��x�ύ��A����1��0����B��1��0������.
��1����������κ����Ĺ�ϵʽ��
��2������һ�뾶Ϊr�ġ�P����Բ��P�����������˶�������P���������ᶼ����ʱ����뾶r��ֵ.
��3���뾶Ϊ1�ġ�P���������ϣ�����P����������ʲô��Χ��ȡֵʱ����P��y�����롢�ཻ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��011-2012ѧ��ɽ��ʡ��ͬ�о��꼶��ѧ�ڵ�һ���¿���ѧ�� ���ͣ������
������12�֣���֪����ȫ�ȵ�ֱ��������ֽƬABC��DEF����ͼ��1�����ã���B��D�غϣ���F��BC�ϣ�AB��EF���ڵ�G����C����EFB��90�㣬��E����ABC��30�㣬AB��DE��4.

1.��1����֤����EGB�ǵ���������
2.��2����ֽƬDEF�������ʡ�ABC�Ƶ�F��ʱ����ת��С ��ʱ���ı���ACDE��Ϊ��EDΪ�����Σ���ͼ��2������������εĸߡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010-2011�꽭��ʡ�����л�ɽ�����꼶��ѧ�����п�����ѧ�� ���ͣ������
������12�֣���֪����ͼ�����κ���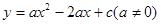 ��ͼ����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0��.
��ͼ����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0��.
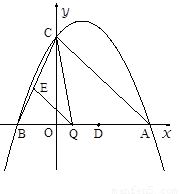
1.��1����ö��κ����Ĺ�ϵʽ��
2.��2��д���ö��κ����ĶԳ���Ͷ������ꣻ
3.��3����Q���߶�AB�ϵĶ��㣬����Q��QE��AC����BC�ڵ�E������CQ.����CQE��������ʱ�����Q�����ꣻ
4.��4����ƽ����x��Ķ�ֱ�� ��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0��.�ʣ��Ƿ����������ֱ��
��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0��.�ʣ��Ƿ����������ֱ�� ��ʹ�á�ODF�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɡ�
��ʹ�á�ODF�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com