
【题目】如图,△ABC中,AB=AC,点P是三角形右外一点,且∠APB=∠ABC.

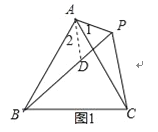
(1)如图1,若∠BAC=60°,点P恰巧在∠ABC的平分线上,PA=2,求PB的长;
(2)如图2,若∠BAC=60°,探究PA,PB,PC的数量关系,并证明;
(3)如图3,若∠BAC=120°,请直接写出PA,PB,PC的数量关系.
【答案】(1)BP=4;(2)PA+PC=PB;(3)![]() PA+PC=PB.
PA+PC=PB.
【解析】
试题分析:(1)AB=AC,∠BAC=60°,证得△ABC是等边三角形,∠APB=∠ABC,得到∠APB=60°,又点P恰巧在∠ABC的平分线上,得到∠ABP=30°,得到直角三角形,利用直角三角形的性质解出结果.
(2)在BP上截取PD,使PD=PA,连结AD,得到△ADP是等边三角形,再通过三角形全等证得结论.
(3)以A为圆心,以AP的长为半径画弧交BP于D,连接AD,过点A作AF⊥BP交BP于F,得到等腰三角形,然后通过三角形全等证得结论.
试题解析:解:(1)∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,∠APB=∠ABC,
∴∠APB=60°,
又∵点P恰巧在∠ABC的平分线上,
∴∠ABP=30°,
∴∠PAB=90°,
∴BP=2AP,
∵AP=2,
∴BP=4;
(2)结论:PA+PC=PB.
证明:如图1,在BP上截取PD,使PD=PA,连结AD,
∵∠APB=60°,
∴△ADP是等边三角形,
∴∠DAP=60°,
∴∠1=∠2,PA=PD,
又AB=AC,
∴△ABD≌△ACP,
∴PC=BD,
∴PA+PC=PB;
(3)结论:![]() PA+PC=PB.
PA+PC=PB.
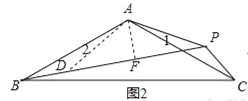
证明:如图2,以A为圆心,以AP的长为半径画弧交BP于D,连接AD,过点A作AF⊥BP交BP于F,
∴AP=AD,
∵∠BAC=120°,
∴∠ABC=30°,
∴∠APB=30°,
∴∠DAP=120°,
∴∠1=∠2,
又AB=AC,
∴△ABD≌△ACP,
∴BD=PC,
∵AF⊥PD,
∴PF=![]() AP,
AP,
∴PD=![]() AP,
AP,
∴![]() PA+PC=PB.
PA+PC=PB.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,正确的个数有( )
①1的算术平方根是1;②(-1)2的算术平方根是-1;③一个数的算术平方根等于它本身,这个数只能是零;④-4没有算术平方根.
A. 1个 B. 2个 C. 3个 D. 4个;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要调查人们对“低碳生活”的了解程度,宜采用普查方式
B. 一组数据3,4,4,6,8,5的众数和中位数都是3
C. 必然事件的概率是100%,随机事件的概率是50%
D. 若甲组数据的方差S甲2=0.128,乙组数据的方差S乙2=0.036;则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.

(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备随机选出七、八、九三个年级各1名学生担任学校国旗升旗手.现已知这三个年级每个年级分别选送一男、一女共6名学生作为备选人.
(1)请你利用树状图或表格列出所有可能的选法;
(2)求选出“一男两女”三名国旗升旗手的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com