
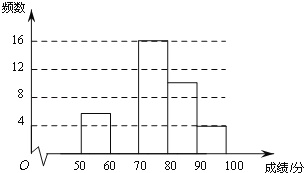
【题目】为弘扬中华传统文化,了解学生整体数学阅读能力,某校组次阅读理解大赛的初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图
分组/分 | 频数 | 频率 | |
A组 | 50≤x<60 | 6 | 0.12 |
B组 | 60≤x<70 | a | 0.28 |
C组 | 70≤x<80 | 16 | 0.32 |
D组 | 80≤x<90 | 10 | 0.20 |
E组 | 90≤x≤100 | 4 | 0.08 |
(1)表中的a= ;抽取部分学生的成绩的中位数在 组;
(2)把上面的频数分布直方图补充完整;
(3)全校总人数为1000人,如果成绩达到90及90分以上者为优秀,可推荐参加决赛,那么请你估计该校进入决赛的学生大约有多少人.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:如果y′=![]() ,那么称点Q为点P的“伴随点”.
,那么称点Q为点P的“伴随点”.
例如:点(5,6)的“伴随点”为点(5,6);点(﹣5,6)的“伴随点”为点(﹣5,﹣6).
(1)直接写出点A(2,1)的“伴随点”A′的坐标.
(2)点B(m,m+1)在函数y=kx+3的图象上,若其“伴随点”B′的纵坐标为2,求函数y=kx+3的解析式.
(3)点C、D在函数y=﹣x2+4的图象上,且点C、D关于y轴对称,点D的“伴随点”为D′.若点C在第一象限,且CD=DD′,求此时“伴随点”D′的横坐标.
(4)点E在函数y=﹣x2+n(﹣1≤x≤2)的图象上,若其“伴随点”E′的纵坐标y′的最大值为m(1≤m≤3),直接写出实数n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新冠肺炎在全球蔓延,粮食安全与国际粮食贸易等问题再次引起广泛的关注,2020年4月4日,国务院联防联控机制召开新闻发布会,介绍疫情期间粮食供给和保障工作情况,农业农村部发展规划司魏百刚给出了定心丸:“我国粮食连年丰收,已连续5年稳定在1.3万亿斤以上,口粮保障绝对安全”,1.3万亿用科学记数法表示为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
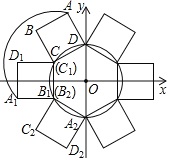
【题目】如图,⊙O的半径为2,圆心O在坐标原点,正方形ABCD的边长为2,点A、B在第二象限,点C、D在⊙O上,且点D的坐标为(0,2),现将正方形ABCD绕点C按逆时针方向旋转150°,点B运动到了⊙O上点B1处,点A、D分别运动到了点A1、D1处,即得到正方形A1B1C1D1(点C1与C重合);再将正方形A1B1C1D1绕点B1按逆时针方向旋转150°,点A1运动到了⊙O上点A2处,点D1、C1分别运动到了点D2、C2处,即得到正方形A2B2C2D2(点B2与B1重合),…,按上述方法旋转2020次后,点A2020的坐标为( )
A.(0,2)B.(2+![]() ,﹣1)
,﹣1)
C.(﹣1﹣![]() ,﹣1﹣
,﹣1﹣![]() )D.(1,﹣2﹣
)D.(1,﹣2﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图象中所反映的过程是:小敏从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中![]() 表示时间,
表示时间,![]() 表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
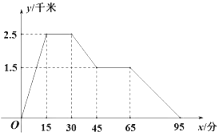
A. 体育场离小敏家2.5千米B. 体育场离早餐店4千米
C. 小敏在体育场锻炼了15分钟D. 小敏从早餐店回到家用时30分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()
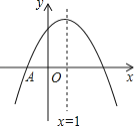
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com