
【题目】已知抛物线y=x2﹣2mx+m2﹣3(m是常数).
(1)证明:无论m取什么实数,该抛物线与x轴都有两个交点;
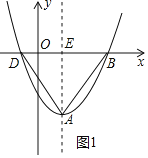
(2)设抛物线的顶点为A,与x轴两个交点分别为B,D,B在D的右侧,与y轴的交点为C.
①求证:当m取不同值时,△ABD都是等边三角形;
②当|m|≤![]() ,m≠0时,△ABC的面积是否有最大值,如果有,请求出最大值,如果没有,请说明理由.
,m≠0时,△ABC的面积是否有最大值,如果有,请求出最大值,如果没有,请说明理由.
【答案】(1)证明见解析;(2)①证明见解析;②![]() .
.
【解析】
(1)令y=0可得出关于x的一元二次方程,由该方程的根的判别式△=12>0,可证出:无论m取什么实数,该抛物线与x轴都有两个交点;
(2)利用二次函数的性质及二次函数图象上点的坐标特征,可求出点A,B,C,D的坐标.
①在Rt△ABE中,利用勾股定理可得出AB=2BE可得出∠BAE=30°,同理,可得出∠DAE=30°及∠BAD=60°,再结合AB=AD即可证出:当m取不同值时,△ABD都是等边三角形;
②分0<m≤![]() 及-
及-![]() ≤m<0两种情况找出S△ABC关于m的函数关系式,利用二次函数的性质或一次函数的性质求出S△ABC的最大值,比较后即可得出结论.
≤m<0两种情况找出S△ABC关于m的函数关系式,利用二次函数的性质或一次函数的性质求出S△ABC的最大值,比较后即可得出结论.
(1)证明:令y=0,则有x2-2mx+m2-3=0.
∵△=(-2m)2-4×1×(m2-3)=12>0,
∴关于x的一元二次方程x2-2mx+m2-3=0有两个不相等的实数根,
∴无论m取什么实数,该抛物线与x轴都有两个交点;
(2)解:∵y=x2-2mx+m2-3=(x-m)2-3,
∴顶点A的坐标为(m,-3),
设抛物线对称轴与x轴的交点为E,则点E的坐标为(m,0);
当x=0时,y=x2-2mx+m2-3=m2-3,
∴点C的坐标为(0,m2-3);
当y=0时,x2-2mx+m2-3=0,即(x-m)2=3,
解得:x1=m-![]() ,x2=m+
,x2=m+![]() ,
,
∴点D的坐标为(m-![]() ,0),点B的坐标为(m+
,0),点B的坐标为(m+![]() ,0).
,0).
①证明:在Rt△ABE中,AE=3,BE=m+![]() -m=
-m=![]() ,
,
∴AB=![]() =2
=2![]() =2BE,
=2BE,
∴∠BAE=30°.
同理,可得出:∠DAE=30°,
∴∠BAD=∠BAE+∠DAE=60°.
又∵AB=AD,
∴当m取不同值时,△ABD都是等边三角形.
②分两种情况考虑:
(i)当0<m≤![]() 时,如图2所示.
时,如图2所示.
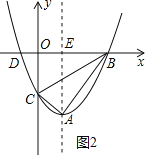
S△ABC=S梯形OCAE+S△ABE-S△OCB,
=![]() OE(OC+AE)+
OE(OC+AE)+![]() AEBE-
AEBE-![]() OCOB,
OCOB,
=![]() m(3-m2+3)+
m(3-m2+3)+![]() ×3×(m+
×3×(m+![]() -m)-
-m)-![]() (3-m2)(m+
(3-m2)(m+![]() ),
),
=![]() m2+
m2+![]() m=
m=![]() (m+
(m+![]() )2-
)2-![]() ,
,
∵![]() >0,
>0,
∴当0<m≤![]() 时,S△ABC随m的增大而增大,
时,S△ABC随m的增大而增大,
∴当m=![]() 时,S△ABC取得最大值,最大值为3
时,S△ABC取得最大值,最大值为3![]() ;
;
(ii)当-![]() ≤m<0时,如图3所示.
≤m<0时,如图3所示.
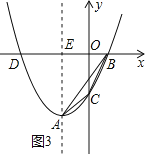
S△ABC=S梯形EACO+S△OCB-S△ABE,
=![]() OE(OC+AE)+
OE(OC+AE)+![]() OCOB-
OCOB-![]() AEBE,
AEBE,
=-![]() m(3-m2+3)+
m(3-m2+3)+![]() (3-m2)(m+
(3-m2)(m+![]() )-
)-![]() (m+
(m+![]() -m)(3-m2)=-
-m)(3-m2)=-![]() m,
m,
∵-![]() <0,
<0,
∴当-![]() ≤m<0时,S△ABC随m的增大而减小,
≤m<0时,S△ABC随m的增大而减小,
∴当m=-![]() 时,S△ABC取得最大值,最大值为
时,S△ABC取得最大值,最大值为![]() .
.
∵3![]() >
>![]() ,
,
∴当m=![]() 时,△ABC的面积取得最大值,最大值为3
时,△ABC的面积取得最大值,最大值为3![]() .
.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
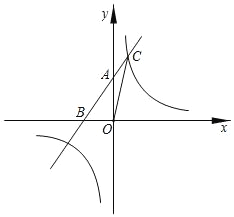
【题目】如图,直线y=x+2与坐标轴相交于A,B两点,与反比例函数y=![]() 在第一象限交点C(1,a).求:
在第一象限交点C(1,a).求:
(1)反比例函数的解析式;
(2)△AOC的面积;
(3)不等式x+2﹣![]() <0的解集(直接写出答案)
<0的解集(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
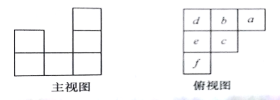
【题目】用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:
(1)求![]() 的值;
的值;
(2)这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;
(3)当![]() 时画出这个几何体的左视图.
时画出这个几何体的左视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
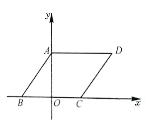
【题目】如图,平行四边形ABCD在平面直角坐标系中,AD=6,若OA,OB的长是关于x的一元二次方程![]() 的两个根,且OA>OB.
的两个根,且OA>OB.
(1)若点E为x轴上的点,且△AOE的面积为![]() .
.
求:①点E的坐标;②证明:△AOE∽△DAO;
(2)若点M在平面直角坐标系中,则在直线AB上是否存在点F,使以A,C,F,M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2x+k=0.
(1)若方程有实数根,求k的取值范围;
(2)如果k是满足条件的最大的整数,且方程x2-2x+k=0一根的相反数是一元二次方程(m-1)x2-3mx-7=0的一个根,求m的值及这个方程的另一根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.
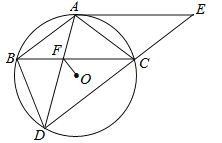
(1)求证:四边形ABCE是平行四边形;
(2)若AE=6,CD=5,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
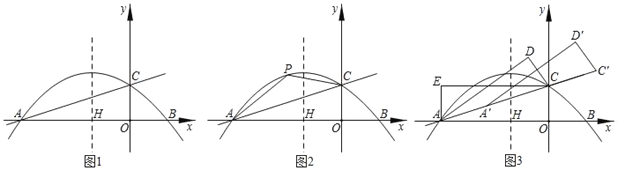
【题目】已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
(1)求直线AC的解析式;
(2)如图2,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M,当四边形AOCP面积最大时,求|PM﹣OM|的最大值.
(3)如图3,将△AOC沿直线AC翻折得△ACD,再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点D′,使得△A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com