
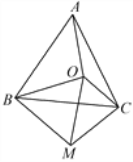
【题目】如图,点![]() 为等边三角形
为等边三角形![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,以
,以![]() 为一边作
为一边作![]() ,且
,且![]() ,连接
,连接![]() 、
、![]() .
.
(1)判断![]() 与
与![]() 的大小关系并证明;
的大小关系并证明;
(2)若![]() ,
,![]() ,
,![]() ,判断
,判断![]() 的形状并证明.
的形状并证明.
【答案】(1)AO=CM,见解析;(2)△OMC是直角三角形,见解析.
【解析】
(1)可证出△OBM是等边三角形,得出OM=OB=BM,由∠ABC=∠OBM得出∠ABO=∠CBM,根据SAS证明△AOB≌△CMB,即可得出结论;
(2)由勾股定理的逆定理即可得出结论.
解:(1)AO=CM;理由如下:
∵∠OBM=60°,OB=BM,
∴ △OBM是等边三角形
∴ OM=OB=BM,
∠ABC=∠OBM=60°
∴∠ABO=∠CBM,
在△AOB和△CMB中,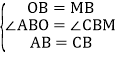 ,
,
∴△AOB≌△CMB(SAS),
∴ AO=CM;
(2)△OMC是直角三角形;理由如下:
在△OMC中,OM2=100,OC2+CM2=62+82=100,
∴OM2=OC2+CM2,
∴△OMC是直角三角形.
故答案为:(1)AO=CM,见解析;(2)△OMC是直角三角形,见解析.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校图书馆大楼工程在招标时,接到甲乙两个工程队的投标书,每施工一个月,需付甲工程队工程款16万元,付乙工程队12万元。工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:
(1)甲队单独完成此项工程刚好如期完工;
(2)乙队单独完成此项工程要比规定工期多用3个月;
(3)若甲乙两队合作2个月,剩下的工程由乙队独做也正好如期完工。
你觉得哪一种施工方案最节省工程款,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王同学准备筹集资金为贫困山区儿童捐款,打算从淘宝网上购进一批闪光发箍和荧光棒在某演唱会现场出售,其中闪光发箍的购买价格为6元/个,荧光棒的购买价格为8元/个.
(1)小王计划购进闪光发箍和荧光棒共120个,且将闪光发箍加价40%、荧光棒加价20%后出售.当所有物品售完后,若利润不低于256元,则小王至少应购买闪光发箍多少个?
(2)小王调整了方案,决定将闪光发箍的售价在进价的基础上上涨(a+10)%、荧光棒的售价在进价基础上上涨a%,在(1)中闪光发箍购买量取得最小值的情况下,将闪光发箍的购买量提![]() a%,而荧光棒的购买量保持不变,则全部售出后,最终可获利246.4元,请求出a的值.
a%,而荧光棒的购买量保持不变,则全部售出后,最终可获利246.4元,请求出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决问题:
我们把一个能被17整除的自然数称为“节俭数”,“节俭数”的特征是:若把一个自然数的个位数字截去,再把剩下的数减去截去的那个个位数字的5倍,如果差是17的整数倍(包括0),则原数能被17整除.如果差太大或心算不易看出是否是17的倍数,就继续上述的“截尾、倍大、相减、验差”的过程,直到能清楚判断为止.
例如:判断1675282是不是“节俭数”.判断过程:167528﹣2×5=167518,16751﹣8×5=16711,1671﹣1×5=1666,166﹣6×5=136,到这里如果你仍然观察不出来,就继续13﹣6×5=﹣17,﹣17是17的整数倍,所以1675282能被17整除.所以1675282是“节俭数”.
(1)请用上述方法判断7259和2098752 是否是“节俭数”,并说明理由;
(2)一个五位节俭数![]() ,其中个位上的数字为b,十位上的数字为a,请求出这个数.
,其中个位上的数字为b,十位上的数字为a,请求出这个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车和一辆快车沿相同的路线从A地到B地,所行驶的路程与时间的函数图形如图所示,下列说法正确的有( )
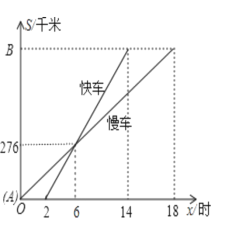
①快车追上慢车需6小时;②慢车比快车早出发2小时;③快车速度为46km/h;④慢车速度为46km/h; ⑤A、B两地相距828km;⑥快车从A地出发到B地用了14小时
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
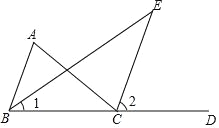
【题目】如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.
(1)求证:∠A=2∠E,以下是小明的证明过程,请在括号里填写理由.
证明:∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,(已知)
∴∠ACD=∠ABC+∠A,∠2=∠1+∠E(_________)
∴∠A=∠ACD﹣∠ABC,∠E=∠2﹣∠1(等式的性质)
∵CE是外角∠ACD的平分线,BE是∠ABC的平分线(已知)
∴∠ACD=2∠2,∠ABC=2∠1(_______)
∴∠A=2∠2﹣2∠1(_________)
=2(∠2﹣∠1)(_________)
=2∠E(等量代换)
(2)如果∠A=∠ABC,求证:CE∥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(s),y=PC2,则y关于x的函数的图像大致为 ( )
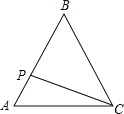
A. 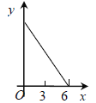 B.
B. 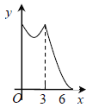 C.
C. 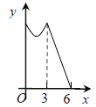 D.
D. 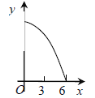
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com