练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．已知图形B是一个正方形，图形A由三个图形B构成，如图，请用图形A与B拼接，并分别画在从左至右的网格中．

    （1）拼得的图形是轴对称图形；
    （2）拼得的图形是中心对称图形．

    分析 （1）直接利用轴对称图形的定义得出符合题意的图形；
    （2）直接利用中心对称图形的定义得出符合题意的图形．

    解答 解：（1）如图1所示：标号1，2，3，4都是符合题意的位置，答案不唯一；

    （2）如图2所示：标号1，2，3都是符合题意的位置，答案不唯一．

    点评 此题主要考查了轴对称图形以及中心对称图形的性质，正确把握定义是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．平行四边形ABCD的对角线AC与BD相交于点O，∠ADB=90°，OA=5，OB=3，求AD和AC的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，直线y=$\frac{1}{2}$x+2分别与x轴、y轴相交于点A、点B．
    （1）求点A和点B的坐标；
    （2）若点P是y轴上的一点，设△AOB、△ABP的面积分别为S△AOB与S△ABP，且S△ABP=2S△AOB，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

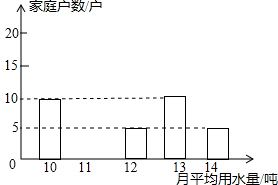    5．为了倡导“节约用水，从我做起”，南沙区政府决定对区直属机关300户家庭的用水情况作一次调查，区政府调查小组随机抽查了其中50户家庭一年的月平均用水量（单位：吨），调查中发现每户用水量均在10-14吨/月范围，并将调查结果制成了如图所示的条形统计图．
    （1）请将条形统计图补充完整；
    （2）这50户家庭月用水量的平均数是11.6，众数是11，中位数是11；
    （3）根据样本数据，估计南沙区直属机关300户家庭中月平均用水量不超过12吨的约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．数学老师布置了这样一道作业题：
    在△ABC中，AB=AC≠BC，点D和点A在直线BC的同侧，BD=BC，∠BAC=α，∠DBC=β，α+β=120°，连接AD，求∠ADB的度数．
    小聪提供了研究这个问题的过程和思路：先从特殊问题开始研究，当α=90°，β=30°时（如图1），利用轴对称知识，以AB为对称轴构造△ABD的轴对称图形△ABD′，连接CD′（如图2），然后利用α=90°，β=30°以及等边三角形的相关知识便可解决这个问题．

    （1）请结合小聪研究问题的过程和思路，求出这种特殊情况下∠ADB的度数；
    （2）结合小聪研究特殊问题的启发，请解决数学老师布置的这道作业题；
    （3）解决完老师布置的这道作业题后，小聪进一步思考，当点D和点A在直线BC的异侧时，且∠ADB的度数与（1）中相同，则α，β满足的条件为0°＜α＜180°，β=60°或120°＜α＜180°，α-β=120°（直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．平行四边形一边的长是10cm，那么它的两条对角线长可以是（　　）
    A．4、6cmB．6、8cmC．8、12cmD．20、30cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知：OP平分∠AOB，∠DCE的顶点C在射线OP上，射线CD交射线OA于F，射线CE交射线OB于G．
    （1）如图①，若CD⊥OA，CE⊥OB，请直接写出线段CF与CG的数量关系：CF=CG；
    （2）如图②，若∠AOB=120°，∠DCE=∠AOC，试判断线段CF与线段CG的数量关系并加以证明；
    （3）若∠AOB=α，当∠DCE满足什么条件时，你在（2）中得到的结论仍然成立，请直接写出∠DCE满足的条件．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

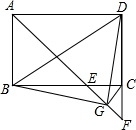    20．如图，在矩形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于点F，取EF的中点G，连接CG，BG，BD，DG，下列结论：
    ①BE=CD；
    ②∠DGF=135°；
    ③△BEG≌△DCG；
    ④∠ABG+∠ADG=180°；
    ⑤若$\frac{AB}{AD}$=$\frac{2}{3}$，则3S△BDG=13S△DGF．
    其中正确的结论是①③④⑤．（请填写所有正确结论的序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．在如图所示的直角坐标系中，解答下列问题：
    （1）分别写出点A、B的坐标；
    （2）将△ABC绕点A顺时针旋转90°，画出旋转后的△AB1C1；
    （3）求线段BB1所在直线的解析式．

    查看答案和解析>>

    同步练习册答案