
如图,将正方形ABCD的四个顶点,分别沿着边逆时针平移,如A移动到E,并使移动的距离都等于AE,得到新四边形EFGH,量椓浚?阋凰悖?卸—EFGH是什么四边形.
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
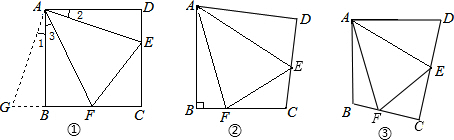
 (1)如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7:
(1)如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7: 0°)绕点B按顺时针转动一个角度到A1BC1的位置,使得点A、B、C1在同一条直线上,那么这个角度等于
0°)绕点B按顺时针转动一个角度到A1BC1的位置,使得点A、B、C1在同一条直线上,那么这个角度等于查看答案和解析>>
科目:初中数学 来源: 题型:
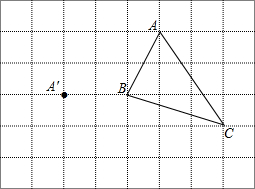 如图,将三角形ABC进行平移,使点A的对应点为点A′
如图,将三角形ABC进行平移,使点A的对应点为点A′查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省盐城市建湖县近湖中学九年级(上)数学周练作业(4)(解析版) 题型:解答题
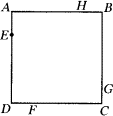
 ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想. ∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com