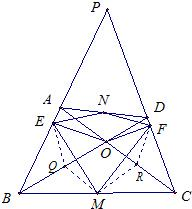
(1)证明:设Q,R分别是OB,OC的中点,连接EQ,MQ,FR,MR,如图,
∴
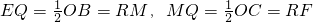
,四边形OQMR是平行四边形,
∴∠OQM=∠ORM,
而A,B,C,D四点共圆,
∴∠ABD=∠ACD,
∴∠EQO=2∠ABD=2∠ACD=∠FRO,
所以∠EQM=∠EQO+∠OQM=∠FRO+∠ORM=∠FRM,
∴△EQM≌△MRF,
∴EM=FM,
同理可得EN=FN,
所以EM•FN=EN•FM.
(2)若EM•FN=EN•FM,不一定有A,B,C,D四点共圆.理由如下:
当AD∥BC时,由于∠B≠∠C,所以A,B,C,D四点不共圆,但此时仍然有EM•FN=EN•FM,证明如下:
如图2所示,
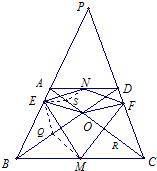
设S,Q分别是OA,OB的中点,连接ES,EQ,MQ,NS,则
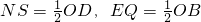
,
∴
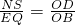
.①
又∵
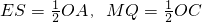
,
∴
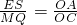
.②
而AD∥BC,所以
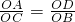
,③
由①,②,③得
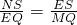
.
∵∠NSE=∠NSA+∠ASE=∠AOD+2∠AOE,∠EQM=∠MQO+∠OQE=(∠AOE+∠EOB)+(180°-2∠EOB)=∠AOE+(180°-∠EOB)=∠AOD+2∠AOE,
即∠NSE=∠EQM,
∴△NSE∽△EQM,
故
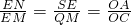
(由②).
同理可得,
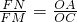
,
所以
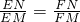
,
从而EM•FN=EN•FM.
分析:(1)设Q,R分别是OB,OC的中点,连接EQ,MQ,FR,MR,如图,则
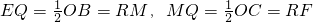
,四边形OQMR是平行四边形,得到∠OQM=∠ORM,而A,B,C,D四点共圆,有∠ABD=∠ACD,得到∠EQM=∠EQO+∠OQM=∠FRO+∠ORM=∠FRM,得到
△EQM≌△MRF,则EM=FM,同理可得EN=FN,即可得到结论.
(2)若EM•FN=EN•FM,不一定有A,B,C,D四点共圆.当AD∥BC时,由于∠B≠∠C,所以A,B,C,D四点不共圆,但此时仍然有EM•FN=EN•FM.设S,Q分别是OA,OB的中点,连接ES,EQ,MQ,NS,则
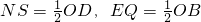
,得到
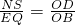
.①
同理得
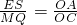
.②而AD∥BC,所以
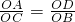
③,易证∠NSE=∠EQM,则△NSE∽△EQM,得到
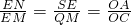
(由②).同理可得,
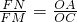
,所以
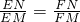
,从而EM•FN=EN•FM.
点评:本题考查了四点共圆的判定与性质;也考查了三角形中位线的性质和斜边上的中线性质以及三角形全等和相似的判定与性质.

 (1)证明:设Q,R分别是OB,OC的中点,连接EQ,MQ,FR,MR,如图,
(1)证明:设Q,R分别是OB,OC的中点,连接EQ,MQ,FR,MR,如图,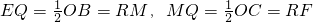 ,四边形OQMR是平行四边形,
,四边形OQMR是平行四边形,
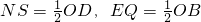 ,
,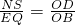 .①
.①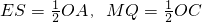 ,
,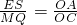 .②
.②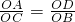 ,③
,③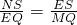 .
.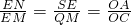 (由②).
(由②).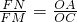 ,
,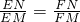 ,
,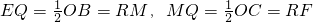 ,四边形OQMR是平行四边形,得到∠OQM=∠ORM,而A,B,C,D四点共圆,有∠ABD=∠ACD,得到∠EQM=∠EQO+∠OQM=∠FRO+∠ORM=∠FRM,得到
,四边形OQMR是平行四边形,得到∠OQM=∠ORM,而A,B,C,D四点共圆,有∠ABD=∠ACD,得到∠EQM=∠EQO+∠OQM=∠FRO+∠ORM=∠FRM,得到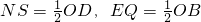 ,得到
,得到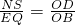 .①
.①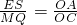 .②而AD∥BC,所以
.②而AD∥BC,所以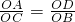 ③,易证∠NSE=∠EQM,则△NSE∽△EQM,得到
③,易证∠NSE=∠EQM,则△NSE∽△EQM,得到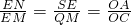 (由②).同理可得,
(由②).同理可得,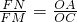 ,所以
,所以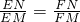 ,从而EM•FN=EN•FM.
,从而EM•FN=EN•FM.
