
【题目】如图1,在平行四边形ABCD中,E,F分别在边AD,AB上,连接CE,CF,且满足∠DCE=∠BCF,BF=DE,∠A=60°,连接EF.
(1)若EF=2,求△AEF的面积;
(2)如图2,取CE的中点P,连接DP,PF,DF,求证:DP⊥PF.

【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】分析:(1)先证明△CDE≌△CBF,得到CD=CB,可得ABCD是菱形,则AD=AB,由DE=BF得AE=AF,则△AEF是等边三角形,根据EF的长可得△AEF的面积;
(2)延长DP交BC于N,连结FN,证明△CPN≌△EPD,得到AE=BN,证明△FBN≌△DEF,得到FN=FD,根据等腰三角形三线合一的性质可得结论.
详解:(1)∵四边形ABCD是平行四边形,
∴∠D=∠B,
∵BF=DE,∠DCE=∠BCF,
∴△CDE≌△CBF(AAS),
∴CD=CB,
∴ABCD是菱形,
∴AD=AB,
∴AD﹣DE=AB﹣BF,即AE=AF,
∵∠A=60°,
∴△AEF是等边三角形,
∵EF=2,
∴S△AEF=![]() ×22=
×22=![]() ;
;
(2)证明:如图2,延长DP交BC于N,连结FN,

∵四边形ABCD是菱形,
∴AD∥BC,
∴∠EDP=∠PNC,∠DEP=∠PCN,
∵点P是CE的中点,
∴CP=EP.
∴△CPN≌△EPD,
∴DE=CN,PD=PN.
又∵AD=BC.
∴AD﹣DE=BC﹣CN,即AE=BN.
∵△AEF是等边三角形,
∴∠AEF=60°,EF=AE.
∴∠DEF=120°,EF=BN.
∵AD∥BC,
∴∠A+∠ABC=180°,
又∵∠A=60°,
∴∠ABC=120°,
∴∠ABC=∠DEF.
又∵DE=BF,BN=EF.
∴△FBN≌△DEF,
∴DF=NF,
∵PD=PN,
∴PF⊥PD.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线于点F,已知∠F=40°,则∠E=_____度.

【答案】80
【解析】
如图,根据角平分线的性质和平行线的性质,可知∠FMA=![]() ∠CPE=∠F+∠1,∠ANE=∠E+2∠1=∠CPE,即∠E=2∠F=2×40°=80°.
∠CPE=∠F+∠1,∠ANE=∠E+2∠1=∠CPE,即∠E=2∠F=2×40°=80°.
故答案为:80.

【题型】填空题
【结束】
14
【题目】如图,点P从![]() 出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,BC=CD,E,F,G,H分别为AB,BC,CD,AD的中点,顺次连接E,G,F,H,求证:四边形EFGH是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+6分别交x轴、y轴于A、B两点,抛物线y=﹣
x+6分别交x轴、y轴于A、B两点,抛物线y=﹣ ![]() x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.
x2+8,与y轴交于点D,点P是抛物线在第一象限部分上的一动点,过点P作PC⊥x轴于点C.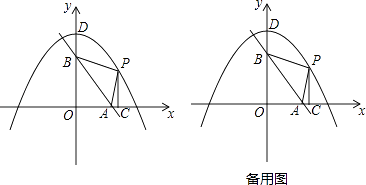
(1)点A的坐标为 , 点D的坐标为;
(2)探究发现:
①假设P与点D重合,则PB+PC=;(直接填写答案)
②试判断:对于任意一点P,PB+PC的值是否为定值?并说明理由;
(3)试判断△PAB的面积是否存在最大值?若存在,求出最大值,并求出此时点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程.
(1)x2﹣14x=8(配方法)
(2)x2﹣7x﹣18=0(公式法)
(3)(2x+3)2=4(2x+3)(因式分解法)
(4)2(x﹣3)2=x2﹣9.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
(1)当a=10米时,花圃的面积=
(2)通道的面积与花圃的面积之比能否恰好等于3:5,如果可以,求出此时通道的宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
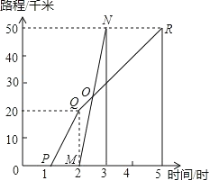
【题目】如图所示 A、B 两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地.如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
(1)甲乙两人中, 先出发,先出发 小时.
(2)甲乙两人中, 先到达B地,先到 小时.
(3)分别求出乙骑摩托车的速度和甲骑自行车在全程的平均速度.
(4)乙出发大约用多长时间就追上甲?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com