
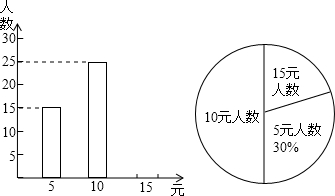
分析 (1)由条形图和扇形图得到捐款“5元人数”以及所占的百分比,计算即可;
(2)求出捐款“15元人数”,补全条形统计图;
(3)根据每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比计算;
(4)计算出50人平均捐款即可.
解答 解:(1)由条形图和扇形图可知,捐款“5元人数”是15人,占30%,
则该班人数为15÷30%=50人;
(2)捐款“15元人数”为50-15-25=10人,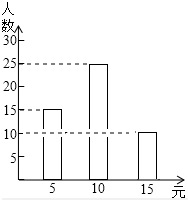
补全条形统计图如图:
(3)捐款“15元人数”所在扇形的圆心角∠AOB的度数为:360°×$\frac{10}{50}$=72°;
(4)50人的捐款数为15×5+25×10+10×15=475,
则50人平均捐款475÷50=9.5元,
该校九年级学生共捐款;9.5×800=7600元.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
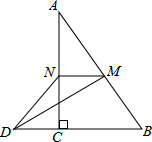 如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DM、DN、MN.若AB=6,则DN=3.
如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DM、DN、MN.若AB=6,则DN=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
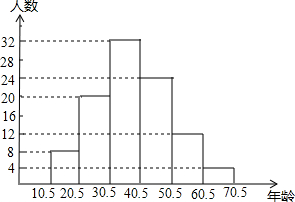 今年6月南博会在我市成功举办,吸引了众多的国内外人士,期间,对六家大宾馆、饭店中游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成条形统计图,如图所示,请结合图形回答下列问题:
今年6月南博会在我市成功举办,吸引了众多的国内外人士,期间,对六家大宾馆、饭店中游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成条形统计图,如图所示,请结合图形回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com